4. Построение комбинационных схем на логических элементах. Технологии минимизации комбинационных схем. Использование диаграмм Вейча для минимизации фал.

Схемы, выходное состояние которых однозначно определяется только комбинацией входных сигналов, называют комбинационными. Закон функционирования КС определяется системой переключательных (логических) функций:

Синтез (построение) комбинационной схемы состоит в построении схемы на основе заданного закона ее функционирования в виде системы переключательных функций (ПФ) или таблиц истинности. При синтезе комбинационной схемы чаще всего необходимо построить схему с использованием минимального числа элементов в заданном элементном базисе, например, на элементах И-НЕ.

Комбинационные схемы строятся из элементарных логических элементов И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и других. Соединяют эти элементы так, как это следует из логической формулы, т.е. вход одного элемента, в котором часть аргументов обработана как указано в формуле, подключается ко входу другого, где выполняется дальнейшая обработка логической функции. В схеме не должно быть обратных связей, т.е. соединения выходов последующих схем со входами предыдущих.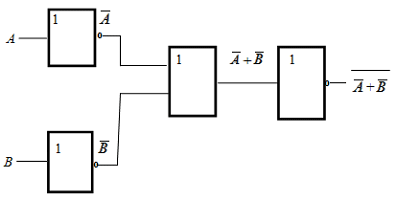

Пример: Пусть дана логическая функция

Комбинационная схема представлена на рисунке.

Этапы синтеза:

1. Задание логической функции словесно, с помощью таблиц истинности или булевых выражений.

2. Минимизация логической функции с помощью алгебраического или графического метода (диаграммы Вейча, карты Карно).

3. Запись булевого выражения минимизированной переключательной функции.

4. Преобразование булевого выражения минимизированной ПФ для реализации её в заданном базисе И-НЕ или ИЛИ-НЕ.

5. Составление функциональной схемы, т.е. изображение нужных логических элементов и связей между ними.

Технологии минимизации. Минимизацией называют процедуру упрощения аналитического выражения, представляющего переключательную (логическую) функцию, направленную на то, чтобы булево выражение ПФ содержало минимальное количество членов с минимальным числом переменных. Способы минимизации: алгебраический; с помощью диаграмм Вейча (карт Карно).

Алгебраический способ минимизации ПФ - используя тождества и теоремы булевой алгебры.

Пример 1. Исходное булево выражение:

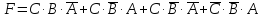
Применяя теорему склеивания , получим булево выражение, которое равносильно (эквивалентно) исходному, но значительно проще его.

Диаграммы Вейча построены так, что их соседние клетки содержат члены исходной ПФ, отличающиеся значением одной переменной: один член содержит эту переменную в прямой форме, а другой – в инверсной. Благодаря этому возникает наглядное представление о различных вариантах склеивания смежных членов.

Исходным продуктом для применения диаграмм Вейча является представление ПФ таблицей истинности, в которой возможные наборы переменных упорядочены по возрастанию или по убыванию их десятичных эквивалентов.

Вид диаграмм Вейча зависит от числа переменных минимизируемой ПФ - n и от того, как упорядочены наборы переменных в таблице. Если наборы упорядочены по возрастанию их десятичных эквивалентов, то диаграммы Вейча для n=2,3,4 имеют вид, приведенный на рисунке.

Число клеток диаграммы равно количеству наборов переменных: Nкл=Nнаб=2ⁿ.

Каждая клетка соответствует определенному набору переменных и имеет номер, одинаковый с номером набора.

Строки и столбцы диаграммы, помеченные чертой, определяют наборы, в которых переменные принимают единичные значения (входят в прямой форме). Строки и столбцы, не помеченные чертой, соответствуют наборам, в которых те же переменные принимают нулевые значения (входят в инверсной форме). В клетки записываются значения ПФ на соответствующем наборе (нулевое или единичное). Если на каком-то наборе функция не определена, то в клетке диаграммы ставится прочерк (или x).

ПФ считается неопределенной, если:

1) данный набор переменных в реальном логическом устройстве невозможен;

2) значение функции на данном наборе безразлично.

После заполнения диаграммы можно приступить непосредственно к минимизации, которую производят по единицам или нулям. В первом случае результатом минимизации будет булево выражение в ДНФ, а во втором – в КНФ.

Краткий алгоритм:

1. Функция, выраженная в СДНФ (СКНФ), записывается в диаграмму Вейча путём проставления единиц (нулей) в соответствующие координаты.

2. Производится объединение единиц (нулей), стоящих рядом, в так называемые m-кубы. Можно объединять единицы (нули), которые образуют правильный прямоугольник, содержащий 2, 4, 8, 16 единиц (нулей).

Замечание. Необходимо объединять максимально возможное количество смежных клеток, содержащих единицы (нули).

Замечание. Одна и та же единица (нуль) может охватываться несколько раз разными кубами.

Замечание. Верхняя и нижняя строки – смежные (можно объединить). Левый и правый столбцы – смежные. Угловые клетки – тоже смежные (диаграмму можно мысленно свернуть в тор).

Замечание. Перед выполнением минимизации в клетки, содержащие прочерки (где ПФ не определена), можно записать дополнительные единицы (нули), что способствует получению более простого конечного булевого выражения. При этом следует помнить, что хотя бы один раз необходимо объединить лишь основные единицы (нули). Дополнительные единицы (нули) могут увеличивать суммарное число единиц (нулей), входящих в куб, то есть уменьшать число переменных в результирующих конъюнкциях (дизъюнкциях).

3. Выписываются координаты получившихся m-кубов.

Объединённая дизъюнкция (конъюнкция) конъюнктивных (дизъюнктивных) координат всех m-кубов и есть минимальная форма.

Целью минимизации является получение минимальной ДНФ или КНФ, содержащей минимум членов с минимальным количеством входящих в них переменных.

Преобразование из базисов СДНФ и СКНФ в базис «Штрих Шеффера» и «Стрелка Пирса» (проверить, работает ли это как для Шеффера, так и для Пирса, сам алгоритм расписан вроде как только для Шеффера):

1. Проставляются скобки;

2. Все знаки конъюнкции и дизъюнкции заменяются на Штрих Шеффера.

Исключение: если вся функция состоит из одной импликанты, то она берётся с отрицанием.

Исключение: В состав функции входит импликанта из одной буквы – эта импликанта берётся с отрицанием.