Таблицы и матрицы переходов:

RS – триггер на эл-тах И-НЕ:
__ S	__ R	Q(t+1)	Q(t)	Q(t+1)	__ S	__ R
0	0	Х	0	0	1	Х
0	1	0	0	1	0	1
1	0	1	1	0	1	0
1	1	Q(t)	1	1	Х	1
JK– триггер:
J	K	Q(t+1)	Q(t)	Q(t+1)	J	K
0	0	Q(t)	0	0	0	А1
0	1	0	0	1	1	А2
1	0	1	1	0	А3	1
1	1	_____ Q(t)	1	1	А4	0
DV– триггер:
D	V	Q(t+1)	Q(t)	Q(t+1)	D	V
0	0	Q(t)	0	0	A1	____ A1В1
1	0	Q(t)	0	1	1	1
0	1	0	1	0	0	1
1	1	1	1	1	А2	А2В2

Для того что бы получить кодированную таблицу переходов счетчика необходимо в одном столбце записать двоичные наборы , представляющих в данной системе кодирования все десятичные цифры. Эти состояния отнесем к моменту времени t-текущее состояние счетчика

Затем в след. столбце напротив каждого двоичного набора предыдущего столбца записывается новое состояние счетчика, в которое он перейдет после поступления считаемого сигнала.(Например, если текущее состояние счетчика Q3Q2Q1Q0=0100(десятичная цифра 4), то новое состояние счетчика, в которое он перейдет, будет равно 1011(десятичная цифра 5 в данной системе кодирования)). Данные состояния будут относиться к моменту времени t+1 и наз. следующим состоянием счетчика.

Для составления функций возбуждения каждого RS(JK)-триггера счетчика необходимо воспользоваться его матрицей переходов

3. Десятичная цифра	Номер набора

   Минимизация функций возбуждения

Представим функции возбуждения в МДНФ с помощью диаграмм Вейча:

1) Составить эталонную диаграмму Вейча, обозначив все поля десятичными цифрами. Эти числа соответствуют десятичной записи двоичного набора конституенты единицы.

2) Занести неопределенные коэффициенты a_ib_i в поля, цифровые обозначения которых совпадают с индексами рассматриваемых коэффициентов. Из таблицы переходов десятичного счетчика в заданном коде есть такие состояния, которые называются запрещенными (в диаграмме Вейча они помечены как Х), они никогда не появляются при правильной работе счетчика.

3) Далее необходимо записать диаграмму Вейча для каждого из входов RS(JK) триггеров.

4) Для каждого из входов получаем вырожденную комбинационную схему (комбинационная схема, в данном случае, - просто определённый сигнал, поданный на вход).

5) Сигнал переноса должен формироваться при переполнении. Рисуем отдельную диаграмму Вейча, куда занесем единицу на том наборе, который соответствует последнему состоянию, а также запрещенные состояния. Остальные клетки диаграммы заполним нулями. Выполнив покрытие единицы, получим минимальное выражение:

30. Счетчики. Реверсивный счетчик. Функция параллельной загрузки. Увеличение разрядности.

Реверсивные счётчики - это счётчики, которые могут перестраиваться. Т.е. может работать в режиме суммирующего счётчика, и с помощью некоторых управляющих сигналов переходить в режим вычитающего.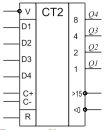

V- реверсивный вход счётчика; D1-D4 – входы предустанова счётчика, С+ С- - входы суммирующие/вычитающие, R – сброс в «0». Выходы >15 и<0 – выходы переполнения/заёма.

УВЕЛИЧЕНИЕ КОЛИЧЕСТВА РАЗРЯДОВ В СЧЁТЧИКЕ:

Чтобы получить один восьмиразрядный счётчик, необходимо либо на вход C+, либо на вход C- первого счётчика подавать входные счётные сигналы - в зависимости от направления счёта. Т.е. необходимо реализовать некоторую комбинационную схему, которая будет подавать счётный сигнал на нужный вход в зависимости от выбранного направления счёта.

Входы переполнения/заёма первого счётчика являются непосредственно счётными сигналами для второго счётчика (который реализует старшие разряды).

Выходы Q1, Q2, Q3, Q4 - это выходы младших разрядов полученного числа; а выходы Q5,Q6 Q7, Q8 - выходы старших разрядов.

Выходы >15 и <0 второго счётчика будут соответствовать переполнению нашего общего счётчика или займу - то есть коду >255 - в случае переполнения; или коду <0 - в случае займа.

Как правило, стандартные счётчики имеют дополнительные входы и выходы, которые позволяют нам

достаточно гибко их комбинировать - для повышения разрядности этой схемы.

ФУНКЦИЯ ПАРАЛЛЕЛЬНОЙ ЗАГРУЗКИ.

Осуществляет установку каждого триггера счётчика в заданное положение. Реализована за счёт дополнительных входов в схеме счётчика управляющих непосредственно триггерами. При этом каждый из входов воздействует на свой триггер, придавая ему заданное значение. Таким образом, можно присвоить счётчику начальное значение и начать отсчёт от него.