Вариант 4

1. Матрицей второго порядка называется:

А) определитель; Б) выражение с двумя элементами; В) таблица из четырех элементов; Г) четыре числа.

2. Результатом сложения двух матриц есть а) матрица того же порядка и размера; б) числовое значение; в) матрица большего размера; г) диагональная матрица.

3.

А) ;

Б) ;

В) ;

Г) .

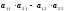4.

А) ;

Б) ;

В) ;

Г) .

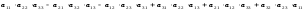5. Матрица любого размера, все элементы которой равны нулю, называется

1. нулевой;

2. единичной;

3. диагональной;

4. вырожденной.

6. Чему равна производная константы?

А) нулю;

Б) единице;

В) константе;

Г) интегралу.

7. Как выглядит формула производной константы?

А) ;

Б) ;

В) ;

Г) .

8. Система линейных уравнений обозначается …

А) круглой скобкой;

Б) квадратной скобкой;

В) фигурной скобкой;

Г) вертикальной чертой.

9. Операция нахождения производной функции называется

А) интегрированием; 

Б) сложением;

В) дифференцированием;

Г) разложением.

10. . Как выглядит формула производной логарифма?

А) ;

Б) ;

В) ;

Г) .

11. Интеграл от логарифма от x по основанию b равен …

А) ∫logb(x)dx=xlogb(x)−logb(e)+C;

Б) ∫exdx=ex+C;

В) ∫adx=a∗x+C;

Г) ∫0dx=C.

12. Интеграл от нуля равен …

А) ∫logb(x)dx=xlogb(x)−logb(e)+C;

Б) ∫exdx=ex+C;

В) ∫adx=a∗x+C;

Г) ∫0dx=C.

13. Иоганна Фридриха Карла Гаусса называют…

А) «королём математиков»;

Б) «принцем»;

В) «величайшим нейробиологом»;

Г) «королём контрастов».

14. Чтобы умножить две матрицы надо..

А) умножить их элементы; Б) строки первой умножить на столбцы второй и просуммировать; В) строки первой умножить на строки второй и просуммировать; Г) их транспонировать и перемножить элементы.

15. Укажите размер матрицы:

А) 2х3; Б) 3х2;

В) 3х3; Г) 2х6;

16. Вычислите определитель третьего порядка: -8+0+0-0-0-15=

А) -23 ;

Б) 23 ;

В) 7 ;

Г) -7 .

17. Дана система уравнений. Найти 1 1 -1

2 0 3

3 -2 0 0+4+9-0-0+6=19

1 1 -2

2 0 8

3 -2 5 0+24+8-0-10+16=38

А) 19,-38,-2;

Б) 19,-19,-1;

В) 19,38,2;

Г) 19,19,1.

18. Найдите производную функции .

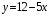А) 7 ^; Б) 12 ; В) -5 ^; Г) -5х ^.

19. Решите систему уравнений

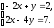
А) (-1; 1,5) ;

Б) (1,5;-1) ;

В) (-3; -2,5) ;

Г) (-2,5; -3) .

20.Записать первые три члена ряда

А) 1,5,6 ;

Б) 3,5,7 ;

В) 3,8,9;

Г) 7,5,11.

Вариант 5

1. Область определения функции имеет вид:

а) ;

б) ;

в) ; г) .

2. Угловой коэффициент касательной к графику функции в точке равен:

а) 2;

б) -1;

в) -4;

г) 4.

3. Дана функция . Установите соответствие между производными функции в соответствующих точках и их значениями:

а) ; Б

б) ; В

в) . А

4. Производная функции имеет вид:

а) ;

б) ;

в) ;

г) .

5. Производная функции в точке равна:

а) 2;

б) 0;

в) ;

г) -2.

6. Производная функции имеет вид:

а) ;

б) ;

в) ;

г) .

7. Точкой минимума функции является:

х²-4х=0 х=4

а) нет экстремума;

б) -2;

в) 4;

г) 0.

8. Если скорость материальной точки, движущейся прямолинейно, равна , тогда путь S, пройденный точкой за время от начала движения, равен:

S=3t+2t²

а) 4;

б) 27;

в) 18;

г) 45.

9. Вторая производная функции 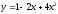имеет вид:

-2+8x

а) ;

б) ;

в) ;

г) .

10. Абсциссой точки перегиба графика функции 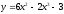является:

12х-6х²

12-12х=0

а) -1;

б) 0;

в) ;

г) 1.

11. Множество всех первообразных функции имеет вид:

а) ;

б) ;

в) ;

г) .

12. Если , тогда функция равна:

а) ;

б) ;

в) ;

г) .

13. Определённый интеграл равен:

а) ;

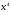б) 15;

в) 36;

г) 17.

14. Используя свойства определённого интеграла, интеграл можно привести к виду:

а) ;

б) ;

в) ;

г) .

15. В результате подстановки интеграл приводится к виду:

а) ;

б) ;

в) ;

г) .

16. Точка для функции является:

а) точкой устранимого разрыва;

б) точкой разрыва I рода;

в) точкой непрерывности;

г) точкой разрыва II рода.

17. Значение предела равно:

а) 0;

б) 3;

в) ;

г) 1.

18. Значение предела равно:

а) -0,5;

б) 0,5;

в) ;

г) 0.

19. Предел равен: _______0.25_______.

20. Значение предела равно:

а) -2;

б) ;

в) 0;

г) .