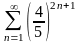- •Первое задание . Кратные интегралы разные
- •Второе задание Ряд Тейлора
- •Ряд Фурье
- •Четвертое задание Степенной ряд
- •Шестое задание Числовые ряды Исследовать на сходимость
- •Седьмое задание Теория
- •229. Задание {{ 686 }} Абс. Сходимость
- •230. Задание {{ 687 }} Предельный признак сравнения
- •Вероятность работы эл. Цепи
- •245. Задание {{ 352 }} тз № 7
- •246. Задание {{ 353 }} тз № 12
- •247. Задание {{ 354 }} тз № 17
- •248. Задание {{ 355 }} тз № 22
- •Вероятность суммы и произведения событий
- •Вероятность хотя бы одного события Дискретная сл. Величина
- •Классическое определение
- •Комбинаторика
- •Математическое ожидание и дисперсия дсв
- •302. Задание {{ 400 }} тз № 32
- •303. Задание {{ 401 }} тз № 33
- •304. Задание {{ 402 }} тз № 34
- •305. Задание {{ 403 }} тз № 35
- •306. Задание {{ 404 }} тз № 31a
- •307. Задание {{ 405 }} тз № 32а
- •Какие из них составлены верно?
- •Непрерывная сл. Величина
- •Определение мат. Ожидания и дисперсии по закону распределения
- •Формулы и определения
Шестое задание Числовые ряды Исследовать на сходимость
217. Задание {{ 701 }} Исследование рядов
Укажите, с помощью какого признака удобнее всего исследовать сходимость каждого из данных рядов
Признак Коши |
|
Признак Даламбера |
|
Признак сравнения в предельной форме |
|
Интегральный признак |
|
Признак Лейбница |
|
218. Задание {{ 702 }} Выбор сходящихся рядов1
Выберите номера сходящихся рядов
1)
 ;
;
2) ;
3) ;
4)
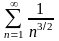 ;
;
5)
 .
.
1)
2)
3)
4)
5)
219. Задание {{ 703 }} Выбор сход. рядов2
Выберите номера сходящихся рядов
1)
 ;
;
2)
 ;
;
3)
 ;
;
4)
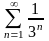 ;
;
5)
 .
.
1)
2)
3)
4)
5)
Седьмое задание Теория
220. Задание {{ 677 }} остаток ряда
Выберете верный ответ (или ответы)
Для сходимости ряда необходимо и достаточно, чтобы
n-ый остаток ряда стремился к нулю при n стремящемся к бесконечности
n-ый остаток ряда стремился к числу R > 0 при n стремящемся к бесконечности
частичные суммы ряда стремились к нулю при n стремящемся к бесконечности
общий член ряда стремился к нулю при n стремящемся к бесконечности
221. Задание {{ 678 }} Коши
Выберете верный ответ (или ответы)
По признаку Коши ряд сходится, если





222. Задание {{ 679 }} Гармонический ряд
Выберите верный ответ
Гармоническим рядом называется ряд вида


223. Задание {{ 680 }} Интегр. признак
Из приведенных формулировок выберите верную
Интегральный признак сходимости числового ряда
формулируется следующим образом:
пусть
дан ряд
 ,
,
тогда если существует функция f(x) со свойствами:
определена и не возрастает при
 ;
;
то
интеграл
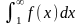 и ряд
и ряд
 сходятся либо расходятся
сходятся либо расходятся
одновременно
определена и не возрастает при
 ;
;
то интеграл и ряд сходятся либо расходятся
одновременно
определена и не убывает при ;
то
интеграл
 и ряд
сходятся либо расходятся
и ряд
сходятся либо расходятся
одновременно
определена и не убывает при ;
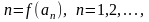
то интеграл и ряд сходятся либо расходятся
одновременно
224. Задание {{ 681 }} определение ряда
Выберете верный ответ (или ответы)
Числовой ряд - это:
Конечная сумма чисел
Бесконечная сумма чисел
Конечная последовательность чисел
Бесконечная последовательность чисел
225. Задание {{ 682 }} Частичная сумма
Выберете верный ответ (или ответы)
Частичная сумма ряда порядка n - это
сумма всех его членов
сумма первых n членов ряда
сумма всех его членов, начиная с n-го
сумма всех его членов, за исключением n-го
226. Задание {{ 683 }} Необх усл сх-ти
Выберете верный ответ (или ответы)
Необходимое условие сходимости числового ряда формулируется в виде:
частичные суммы ряда стремятся к нулю при n стремящемся к бесконечности
частичные суммы ряда ограничены
общий член ряда стремится к нулю при n стремящемся к бесконечности
общий член ряда стремится к пределу q>0 при n стремящемся к бесконечности
227. Задание {{ 684 }} Лейбниц
Выберите верную формулировку признака Лейбница
Ряд
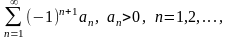 сходится,
если
сходится,
если
выполнены условия:

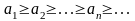



228. Задание {{ 685 }} Признак сравнения
Выберите верные утверждения из приведенных ниже
Пусть
даны ряды
и

и
для всех n = 1,2,…
выполняется неравенство
 Тогда
Тогда
ряды an и bn сходятся или расходятся одновременно
из расходимости ряда an следует сходимость ряда bn
из сходимости ряда bn следует сходимость ряда an
из расходимости ряда bn следует расходимость ряда an
из расходимости ряда an следует расходимость ряда bn