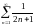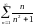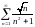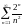Ряд Фурье
165. Задание {{ 727 }} Ряд Фурье четной
Выберите верный ответ
Если
разложение функции
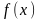в ряд Фурье имеет вид
,
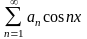то функция
-
четная
нечетная
может быть какой угодно
ни четная, ни нечетная
166. Задание {{ 728 }} Ряд Фурье нечетной ф-ии
Выберите верный ответ
Если разложение функции в ряд Фурье имеет вид
,
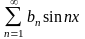то функция
-
четная
нечетная
может быть какой угодно
ни четная, ни нечетная
167. Задание {{ 729 }} "икс квадрат"
Выберите верный ответ
Функция
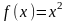разложена
в ряд
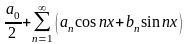
на
интервале
.
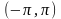Тогда
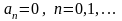
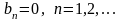
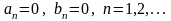
168. Задание {{ 730 }} "икс"
Выберите верный ответ
Функция
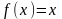разложена
в ряд
на интервале . Тогда
Четвертое задание Степенной ряд
169. Задание {{ 714 }} к теореме Абеля
Выберите верный ответ(ответы)
Ряд по степеням (x-2) cходится в точке x=1 и расходится в точке x=3,5. Тогда он сходится в точке
x=2
x=3/2
x=5/2
x=0
x=4
170. Задание {{ 715 }} Границы инт. сходимости
Выберите верный ответ (ответы)
Ряд по степеням (x-1) имеет радиус сходимости, равный числу 1. Тогда
в точке x=0 он
сходится.
расходится.
может как сходиться, так и расходиться.
171. Задание {{ 717 }} равные инт. сходимости
Выберите верный ответ (ответы)
Степенной ряд по степеням (x-a) и степенной ряд по степеням (x-b) имеют один и тот же интервал сходимости. Тогда совпадают
числа a и b
их радиусы сходимости
их коэффициенты
их суммы
172. Задание {{ 724 }} Нахождение рад. сходимости
Выберите верный ответ (ответы)
Для
степенного ряда
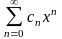имеем
.
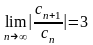Тогда радиус
сходимости этого ряда равен
3
1/3
0
бесконечности
173. Задание {{ 725 }} Вычисл рад. сх-ти№2
Выберите верный ответ (ответы)
Для
степенного ряда
имеем
.
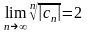Тогда радиус
сходимости этого ряда равен
2
1/2
0
бесконечности
Теория
174. Задание {{ 704 }} равномерная и поточечн. сход-ть
Какие из приведенных утверждений являются верными?
Дан функциональный ряд с областью сходимости Е. Тогда
из поточечной сходимости на Е следует его равномерная сходимость на этом множестве.
из равномерной сходимости на Е следует его поточечная сходимость на этом множестве.
из равномерной сходимости на Е не следует его поточечная сходимость на этом множестве.
из поточечной сходимости на Е не следует его равномерная сходимость на этом множестве.
175. Задание {{ 705 }} Область сход-ти
Выберите верные формулировки
Областью сходимости функционального ряда называется
множество тех значений аргумента, при которых ряд сходится
множество тех значений аргумента, при которых сходится последовательность частичных сумм ряда
множество тех значений аргумента, при которых сходится последовательность членов ряда
176. Задание {{ 706 }} Радиус сходимости
Выберите верные ответы (ответ)
Степенной ряд сходится на всей числовой прямой. Тогда его радиус сходимости равен
некоторому числу R>0.
бесконечности.
нулю.
177. Задание {{ 707 }} Интервал сх-ти
Выберите верный ответ (ответы)
Некоторая функция f(x) разложена в ряд Тейлора по степеням x-2. Тогда интервал сходимости этого ряда может иметь вид
(0;1)
(1;3)
(1;2)
(0;4)
178. Задание {{ 711 }} почленное интегр-е
Выберите верный ответ(ответы)
При почленном интегрировании радиус сходимости степенного ряда
уменьшается
увеличивается
не изменяется
может как увеличиваться, так и уменьшаться
179. Задание {{ 712 }} почленное дифф-е
Выберите верный ответ(ответы)
При почленном дифференцировании радиус сходимости степенного ряда
увеличивается
уменьшается
может как увеличиваться, так и уменьшаться
не изменяется
180. Задание {{ 713 }} Сходимость в одной точке
Выберите верный ответ
Степенной ряд сходится только в одной точке. Тогда его радиус сходимости равен
некоторому числу R>0.
нулю.
бесконечности.
единице.
181. Задание {{ 726 }} функ. ряд-определение
Выберете верный ответ
Функциональный ряд - это
Бесконечная последовательность функций
Бесконечная сумма функций
Конечная сумма функций
Конечная последовательность функций
часть1
182. Задание {{ 316 }} ТЗ № 11
Какой из числовых рядов сходится условно?
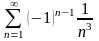
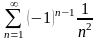
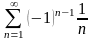
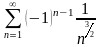
183. Задание {{ 317 }} ТЗ № 12
Какой из числовых рядов сходится абсолютно?
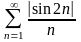
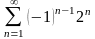
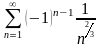
184. Задание {{ 318 }} ТЗ № 13
Длина
интервала сходимости степенного ряда
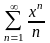равна:
Правильные варианты ответа: 2;
185. Задание {{ 319 }} ТЗ № 14
Длина
интервала сходимости степенного ряда
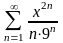равна:
Правильные варианты ответа: 6;
186. Задание {{ 320 }} ТЗ № 15
Длина
интервала сходимости степенного ряда
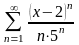равна:
Правильные варианты ответа: 10;
187. Задание {{ 321 }} ТЗ № 16
Коэффициент
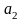в разложении функции
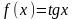в степенной ряд
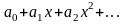равен
Правильные варианты ответа: 0;
188. Задание {{ 322 }} ТЗ № 17
Разложение
функции
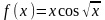в степенной ряд
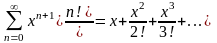
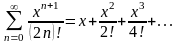
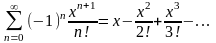
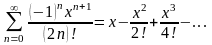
189. Задание {{ 323 }} ТЗ № 18
Разложение
функции
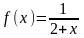в степенной ряд есть
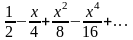
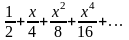
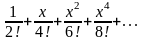
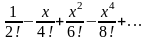
190. Задание {{ 324 }} ТЗ № 19
Вычислить, используя два слагаемых в разложении
подынтегральной функции в степенной ряд и
три знака после запятой в каждом слагаемом
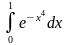
Правильные варианты ответа: 0,8;
191. Задание {{ 325 }} ТЗ № 20
Вычислить, используя два слагаемых в разложении
подынтегральной функции в степенной ряд и
три знака после запятой в каждом слагаемом
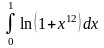
Правильные варианты ответа: 0,057;
192. Задание {{ 326 }} ТЗ № 21
Вычислить, используя два слагаемых в разложении
подынтегральной функции в степенной ряд и
три знака после запятой в каждом слагаемом
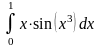
Правильные варианты ответа: 0,185;
ПЯТОЕ ЗАДАНИЕ
часть2
193. Задание {{ 327 }} ТЗ № 1
Ряд сходится, если:
Сумма ряда меньше некоторого числа;
Существуют два числа а и b,
такие, что сумма ряда заключена в
интервале
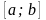
Существует предел последовательности
частичных сумм ряда при
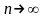
Существует предел общего члена ряда при
194. Задание {{ 328 }} ТЗ № 2
Если
предел общего члена ряда
,
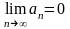то
Ряд сходится
Ряд расходится
Ряд может как сходиться, так и расходиться
Ряд сходится условно
195. Задание {{ 329 }} ТЗ № 3
Если
в ряде с положительными членами
,
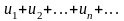
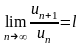то
Ряд сходится, если
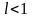
Ряд расходится, если
Ряд сходится, если
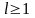
Ряд расходится, если
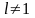
196. Задание {{ 330 }} ТЗ № 4
Ряд называется сходящимся условно, если
Часть его членов положительны, часть - отрицательны
Сходится ряд, составленный из модулей членов
ряда, а исходный ряд - расходится
Сходится исходный ряд, а ряд составленный из
модулей членов исходного ряда - расходится
Сумма ряда, составленного из модулей членов
исходного ряда, ограничена
197. Задание {{ 331 }} ТЗ № 5
Интервалом абсолютной сходимости степенного ряда
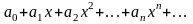называется множество
значений
х, при которых величина
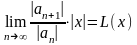
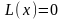
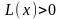
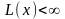
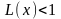
198. Задание {{ 332 }} ТЗ № 6
Рядом Тейлора функции называется выражение вида
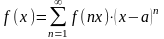
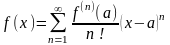
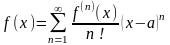
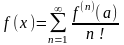
199. Задание {{ 333 }} ТЗ № 10
Сходимость ряда не изменится, если
Взять все его члены по абсолютной величине
Отбросить некоторое конечное число его первых слагаемых
Возвести все члены ряда в квадрат
Начиная с некоторого значения
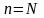заменить
все
члены ряда
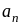на
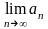
часть3
200. Задание {{ 334 }} ТЗ № 1
Согласно необходимому признаку
сходимости расходится ряд…
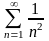
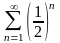
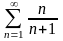
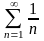
201. Задание {{ 335 }} ТЗ № 22
Согласно необходимому признаку
сходимости расходится ряд…
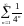
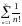
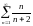
202. Задание {{ 336 }} ТЗ № 2
Какой из числовых рядов расходится?
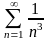
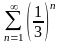
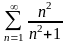
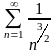
203. Задание {{ 337 }} ТЗ № 23
Согласно необходимому признаку
сходимости расходится ряд…
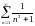
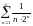
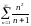
204. Задание {{ 338 }} ТЗ № 3
Какой из числовых рядов расходится?
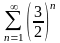
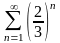
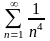
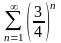
205. Задание {{ 339 }} ТЗ № 24
Согласно необходимому признаку
сходимости расходится ряд…
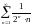
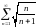
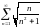
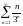
206. Задание {{ 340 }} ТЗ № 4
Какой из числовых рядов сходится?
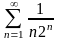
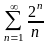
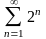
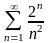
207. Задание {{ 341 }} ТЗ № 25
Какой из числовых рядов сходится?
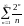
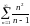
208. Задание {{ 342 }} ТЗ № 5
Какой из числовых рядов сходится?
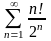
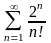
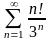
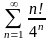
209. Задание {{ 343 }} ТЗ № 26
Какой из числовых рядов сходится?
