Первое задание . Кратные интегралы разные

51. Задание {{ 720 }} Т5Р1№2

1. Двойной интеграл от функции f(x,y)=х·у по области, ограниченной линиями у=0, у=х, х=1 равен

 2

 8



 0

52. Задание {{ 721 }} Т5Р1№4

2. Площадь области, ограниченной линиями у=х+1, х+у=1 и осью Ox равна





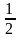
 1



53. Задание {{ 722 }} Т5Р1№1

3. Двойной интеграл от функции f(x,y)=х-у по области, ограниченной линиями х=0, у=0, х=2, у=2 равен

 2

 8

 1

 0

54. Задание {{ 723 }} Т5Р1№3

4. Двойной интеграл от функции f(x,y)=х по области, ограниченной линиями у=х, х+у=2, х=0 равен

 1



 3



55. Задание {{ 724 }} Т5Р1№5

5. Площадь той части плоскости 6х+3у+2z=12, которая заключена в первом квадранте

 10

 14

 1



56. Задание {{ 725 }} Т5Р1№7

6. Тройной интеграл от функции f(x,y,z)=ху по области, ограниченной поверхностями х=1, х=2, у=-2, у=-1, z=0, z=1/2, равен



 1



 0

57. Задание {{ 726 }} Т5Р1№8

7. Тройной интеграл от функции f(x,y,z)=z по области, ограниченной поверхностями х=0, у=0, z=0, х=2, y=2, z=2 равен



 8

 1

 16

58. Задание {{ 727 }} Т5Р1№9

8. Объем тела, ограниченного поверхностями 2х+3у+4z=12, х=0, у=0, z=0 равен

 10

 12

 36

 1

59. Задание {{ 728 }} Т5Р1№10

9. Объем тела, ограниченный поверхностями 4=х²+у², z=2, z=0 равен



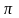
 8

 4

 10

60. Задание {{ 729 }} Т5Р1№6

10. Тройной интеграл по области, ограниченной поверхностями: х=-1, х=1, у=0, у=1, z=0, z=2 от функции f(x,y,z)=х+у-z равен

 1

 2

 -2

 0

Второе задание Ряд Тейлора

154. Задание {{ 708 }} разложение косинуса

Выберите верный ответ(ответы)

Разложение функции cos x в ряд по степеням x имеет вид:

 1+x+x²/2!+…+xⁿ/n!+…

 1-x+x²/2-…+(-1)ⁿ⁺¹xⁿ/n!+…

 1-x²/2!+x⁴/4!-…+(-1)ⁿx²ⁿ/(2n)!+…

 x-x³/3!+x⁵/5!-…+x^2n-1/(2n-1)!+…

155. Задание {{ 709 }} разложение синуса

Выберите верный ответ(ответы)

Разложение функции sin x в ряд по степеням x имеет вид:

 1+x+x²/2!+…+xⁿ/n!+…

 1-x+x²/2-…+(-1)ⁿ⁺¹xⁿ/n!+…

 1-x²/2!+x⁴/4!-…+(-1)ⁿx²ⁿ/(2n)!+…

 x - x³/3!+x⁵/5!-…+ (-1)ⁿ⁺¹x^2n-1/(2n-1)!+…

156. Задание {{ 710 }} разложение логарифма

Выберите верный ответ(ответы)

Разложение функции ln(1+x) в ряд по степеням x имеет вид:

 x-x²/2 +x³/3…+xⁿ/n +…

 1-x+x²/2-…+(-1)ⁿ⁺¹xⁿ/n +…

 1-x²/2!+x⁴/4!-…+(-1)ⁿx²ⁿ/(2n)!+…

 x - x³/3 +x⁵/5 !-…+ (-1)ⁿ⁺¹x^2n-1/(2n-1) +…

 x-x²/2 +x³/3…+(-1)^n-1xⁿ/n +…

 x-x²/2 +x³/3…+(-1)ⁿ xⁿ/n +…

157. Задание {{ 716 }} многочлен Тейлора

Выберите верный ответ (ответы)

Разложение функции по степеням (x-3) имеет вид f(x)=2+4(x-3). Чему равен коэффициент этого разложения с номером n=2?

 4

 0

 2

 3

158. Задание {{ 718 }} геометр. прогрессия-радиус

Выберите верный ответ (ответы)

Радиус сходимости разложения функции 1/(1-x) по степеням x равен

 0

 1

 2

 бесконечности

159. Задание {{ 719 }} разл. косинуса-радиус

Выберите верный ответ (ответы)

Радиус сходимости разложения функции cos x по степеням x равен

 0

 1

 2

 бесконечности

160. Задание {{ 720 }} sin х -радиус сход-ти

Выберите верный ответ (ответы)

Радиус сходимости разложения функции sin x по степеням x равен

 0

 1

 2

 бесконечности

161. Задание {{ 721 }} ln(1+x)-радиус

Выберите верный ответ (ответы)

Радиус сходимости разложения функции ln(1+x) по степеням x равен

 0

 1

 2

 бесконечности

162. Задание {{ 722 }} дифференцируемость суммы ряда

Выберите верный ответ (ответы)

Функция f(x) разлагается в степенной ряд с симметричным относительно

точки x=0 интервалом cходимости (-R; R). Тогда f(x) обязательно является

 четной

 нечетной

 дифференцируемой

 непрерывной

163. Задание {{ 723 }} беск. дифференцируемость суммы ряда

Выберите верный ответ (ответы)

Функция f(x) разложена в степенной ряд в интервале (-R; R). Тогда в этом интервале f(x)

 может не иметь производной

 имеет производные всех порядков

 может быть разрывной

 дифференцируема только один раз

164. Задание {{ 731 }} экспонента

Выберите верный ответ(ответы)

Разложение функции в ряд по степеням x имеет вид:

 1+x+x²/2!+…+xⁿ/n!+…

 1-x²/2!+x⁴/4!-…+x²ⁿ/(2n)!+…

 1-x³/3!+x⁵/5!-…+x^2n-1/(2n-1)!+…

ТРЕТЬЕ ЗАДАНИЕ