
Лабораторные 2, 3, 4 для ВФ по схемотехнике / Лаба2 / Лаба 2
.docxНациональный Исследовательский Ядерный Университет «МИФИ»
Лабораторная работа №2
«Синтез комбинационных схем»
по дисциплине «Схемотехника ЭВМ»
Работу выполнил:
студент группы В5-XXX
Фамилия И.О.
Логин: v5XXXXX
Пароль: XXXXXX
Преподаватель:
Г.Г. Новиков
Н.А. Дмитриев
2011
Цель: изучить методы синтеза комбинационных схем на логических элементах; получить навыки проектирования комбинационных схем на VHDL; овладеть инструментальными средствами проектирования схем на ПЛИС; приобрести опыт экспериментального исследования синтезируемых схем.
Задание. Даны три функции:



Требуется:
-
Провести синтез многовыходной комбинационной схемы;
-
Описать комбинационную схему на VHDL;
-
Получить результаты экспериментальных исследований.
Построим таблицу истинности для трёх заданных функций:
Таблица 1. Таблица истинности трёх функций.
|
№ |
Х3 |
Х2 |
Х1 |
Х0 |
F1 |
F2 |
F3 |
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
2 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
3 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
4 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
|
5 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
|
6 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
7 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
|
8 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
9 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
10 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
11 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
12 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
13 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
|
14 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
|
15 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Запишем СДНФ всех трёх функций:



Получим минимальные ДНФ функций с помощью диаграммы Вейча.
Эталонная диаграмма Вейча:
|
|
|
|
|
||
|
|
13 |
15 |
11 |
9 |
|
|
12 |
14 |
10 |
8 |
|
|
|
|
4 |
6 |
2 |
0 |
|
|
5 |
7 |
3 |
1 |
|
|
|
|
|
|
|
|
|
Диаграмма Вейча для трёх заданных функций:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
1 |
1 |
1 |
|
|
1 |
1 |
1 |
|
|
|
|
|
1 |
|
|
|
||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
1 |
|
|
1 |
|
1 |
|
|
1 |
|
|
1 |
|
|
1 |
|||||||||||||||||||||||
|
1 |
|
|
1 |
|
1 |
|
|
1 |
|
|
1 |
1 |
|
1 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
Диаграмма F1 |
|
Диаграмма F2 |
|
Диаграмма F3 |
||||||||||||||||||||||||||||||||||
Выпишем минимальные ДНФ функций:



Представим функции в базисе «Штрих Шеффера»:



Дадим условные обозначения импликантам и сократим МНДФ:






Тогда функции будут выглядеть так:



Попытаемся уменьшить количество элементов при помощи метода меток.
Логическое произведение функций F1, F2, F3 с помощью диаграммы Вейча:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
1 |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
1 |
|
|
1 |
|
1 |
|
|
1 |
|
|
1 |
|
|
1 |
|||||||||||||||||||||||
|
1 |
|
|
1 |
|
1 |
|
|
1 |
|
|
1 |
|
|
1 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
Диаграмма F1F2 |
|
Диаграмма F1F3 |
|
Диаграмма F2F3 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
Диаграмма F1F2F3 |
|
|
||||||||||||||||||||||||||||||||||
Выпишем простые импликанты данных функций:




Таблица 2. Импликантная матрица.
|
Импликанта |
Конституента |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
F1 |
F2 |
F3 |
F1 |
F2 |
F3 |
F1 |
F2 |
F3 |
F1 |
F2 |
F3 |
F3 |
F1 |
F1 |
F2 |
F2 |
F1 |
F1 |
F2 |
F3 |
|
|
|
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
+ |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
+ |
|
|
+ |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
+ |
|
|
v |
v |
v |
v |
v |
v |
v |
v |
v |
v |
v |
v |
v |
v |
v |
v |
v |
v |
v |
v |
v |


















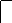






























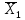
































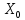




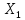













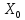













 F1F2F3
F1F2F3 F1F2F3
F1F2F3 F1F2
F1F2 F1
F1 F1
F1 F2
F2 F3
F3