4.Дискретное преобразование Фурье и алгоритм бпф. Фильтровая интерпретация и применение.

Пара непрерывного преобразования Фурье (интеграл Фурье) имеет вид:

(1)

где  – спектр сигнала   (в общем случае и сигнал и спектр — комплексные).

Выражения для прямого ДПФ и обратного дискретного преобразования Фурье (ОДПФ) имеют вид:

(2)

Выражение для ДПФ ставит в соответствие   отсчетам сигнала  ,  , в общем случае комплексного,   отсчетов спектра  ,  .

Можно обратить внимание, что как и в непрерывном, так и в дискретном случае, в выражении для обратного преобразования имеется нормировочный коэффициент. В случае интеграла Фурье это  , в случае ОДПФ –  . Можно отметить, что в случае непрерывного преобразования нормировочный коэффициент 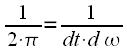  призван корректно отображать масштабирование сигнала во времени в частотную область и наоборот. Другими словами, если последовательно рассчитать спектр некоторого сигнала, а после взять обратное преобразование Фурье, то результат обратного преобразования должен полностью совпадать с исходным сигналом. Нормировочный коэффициент   уменьшает амплитуду сигнала на выходе обратного преобразования для того чтобы она совпадала с амплитудой исходного сигнала.

Рассмотрим теперь сигнал  , как результат умножения непрерывного сигнала   на решетчатую функцию

,

(3)

где   – дельта-функция,

(4)

– интервал дискретизации. Графически процесс дискретизации можно представить как это показано на рисунке 1.

  Рисунок 1: Процесс дискретизации сигнала

Вычислим спектр дискретного сигнала, для этого подставим выражения для дискретного сигнала (3) в выражения для преобразования Фурье (1), получим:

(5)

Поменяем местами операции суммирования и интегрирования и вспомним фильтрующее свойство дельта-функции:

.

(6)

Тогда выражение (5) с учетом (6):

Распространенным способом анализа дискретных цифровых последовательностей является z-преобразование (z-transform).

Произвольной непрерывной функции s(t), равномерно дискретизированной и отображенной отсчетами s_k = s(kt), равно как и непосредственно дискретной функции, можно поставить в соответствие степенной полином по z, последовательными коэффициентами которого являются значения s_k:

s_k = s(kt)  TZ[s(kt)] = s_k z^k = S(z).

где z = +j = rexp(-j) - произвольная комплексная переменная. Полином S(z) называют z-образом или z-изображением функции s(kt). Преобразование имеет смысл для области тех значений z, в которой ряд S(z) сходится, т.е. сумма ряда представляет собой аналитическую функцию переменной z, не имеющую полюсов и особых точек.

Дискретное преобразование Фурье является частным случаем z-преобразования при z = exp(-jt). В общем виде:

S() = S(z), z = exp(-jt);

Обратное преобразование:

S(z) = S(),  = ln z/jt;

Быстрое преобразование Фурье (БПФ, fast Fourier transform - FFT). Он базируется на том, что при вычислениях среди множителей (синусов и косинусов) есть много периодически повторяющихся значений (в силу периодичности функций). Алгоритм БПФ группирует слагаемые с одинаковыми множителями в пирамидальный алгоритм, значительно сокращая число умножений за счет исключения повторных вычислений. В результате быстродействие БПФ в зависимости от N может в сотни раз превосходить быстродействие стандартного алгоритма. При этом следует подчеркнуть, что алгоритм БПФ даже точнее стандартного, т.к. сокращая число операций, он приводит к меньшим ошибкам округления.

Допустим, что массив чисел s_k содержит N = 2^r отсчетов (r - целое). Разделим исходный массив на два первых промежуточных массива с четными и нечетными отсчетами:

s_k' = s_2k, s_k" = s_2k+1, 0  k  N/2-1.

Выполним ДПФ каждого массива с учетом того, что шаг функций равен 2 (при t=1), а период промежуточных спектров будет соответственно равен N/2:

s_k'  S_n', s_k"  S_n", 0  n  N/2-1.

Для получения одной половины искомого спектра S_n сложим полученные спектры с учетом теоремы запаздывания, т.к. отсчеты функции s_k" сдвинуты относительно s_k' на один шаг дискретизации:

S_n = S_n'+S_n"exp(-j2n/N).

Вторая половина спектра, комплексно сопряженная с первой, с учетом периода повторения N/2 промежуточных спектров определяется выражением:

S_n+N/2 = S_n'+S_n"exp(-j2n+N/2)/N) = S_n'- S_n"exp(-j2n/N).

Нетрудно видеть, что для вычисления полного спектра в данном случае потребуется N²/4 операций для вычисления промежуточных спектров плюс еще N операций комплексного умножения и сложения, что создает ощутимый эффект по сравнению с ДПФ.

Но деление массивов на две части может быть применено и к первым промежуточным массивам, и ко вторым, и т.д. до тех пор, пока в массивах не останется по одному отсчету, фурье - преобразование которых равно самому отсчету. Тем самым, алгоритм преобразования превращается в пирамидальный алгоритм перестановок со сложением/вычитанием и с единичным умножением на значение exp(-j2n/N) соответствующего уровня пирамиды. Первый алгоритм БПФ на данном принципе (из множества модификаций, существующих в настоящее время) был разработан Кули-Тьюки в 1965 г. и позволил повысить скорость вычислений в N/r раз по сравнению с ДПФ. Чем больше N, тем больше эффект БПФ. Так, при N = 1024 имеем r = 10 и соответственно N/r 100. Что касается условия по количеству точек N = 2^r, то оно рассматривается в варианте N_k 2^r, где r - минимальное целое. Массивы с N_k < 2^r дополняется до 2^r нулями, что не изменяет форму спектра. Изменяется только шаг  по представлению спектра (= 2/2^r < 2/N), который несколько избыточен по адекватному представлению сигнала в частотной области. В настоящее время существуют и алгоритмы БПФ с другими основаниями и их комбинациями, при которых не требуется дополнения сигналов нулями до 2^r.