2. Вероятностные характеристики обнаружения р/л сигналов. Оптимальная фильтрация сигналов.

Условные вероятности

При обнаружении возможны два неизвестных и взаимоисключающих условия, которые иногда именуются альтернативными гипотезами: условие H₀ – сигнал (цель) есть и условие H₂ – сигнал (цель) отсутствует.

Приемник должен вынести решение о наличии или отсутствии сигнала. Решения обозначим A₁ – сигнал есть и A₀ – сигнал отсутствует.

Существуют четыре варианта совмещения решения и условия:

1) A₁H₁ – правильное обнаружение.

Тогда D = p(A₁|H₁) – вероятность правильного обнаружения.

2) A₀H₁ – пропуск цели.

Тогда D` = p(A₀|H₁) – вероятность пропуска цели.

D + D` = 1.

3) A₁H₀ – ложная тревога.

Тогда F = p(A₁|H₀) – вероятность ложной тревоги.

4) A₀H₀ – правильное необнаружение.

Тогда F` = p(A₀|H₀) – вероятность правильного необнаружения.

F + F` = 1.

Таким образом, существуют 2 вида ошибок – ложная тревога и пропуск цели. Степень нежелательности этих ошибок различна, что надо учитывать при принятии решения. Делается это с помощью некоторой величины – стоимости ошибок. Систему обнаружения характеризуют средней стоимостью (средним риском):

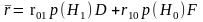
где r₀₁ – стоимость пропуска, r₁₀ – стоимость ложной тревоги, p(H₁) – вероятность наличия сигнала, p(H₀) – вероятность отсутствия сигнала.

Критерии оптимальности обнаружения

Для использования минимума среднего риска в качестве критерия обнаружения (критерий Байеса) должны быть установлены r₀₁ и r₁₀ и известны p(H₁) и p(H₀). Если r₀₁ = r₁₀ = 1, то средний риск равен

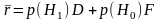
Условие минимума этой суммарной вероятности ошибки называется критерием идеального наблюдателя.

Если подставить D` = 1 – D в исходную формулу, получим:

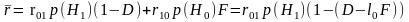
где весовой множитель .

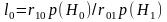Следствием минимума среднего риска является весовой критерий:

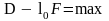
В задачах радиолокации, когда наличие цели встречается сравнительно редко и трудно судить о стоимости пропуска цели, более важную роль играет стоимость ложной тревоги. Она особенно опасна, так как может, например, привести к увеличению числа операций ЭВМ, а также другим действиям, имеющим высокую стоимость. Поэтому в радиолокации задаются заметно меньшей вероятностью ложные тревоги относительно вероятности пропуска цели, т.е. F<<1 – D, и требуют максимизации вероятности D, которая должна быть близкой к единице. Например, по одной из рекомендаций ICAO для РЛС УВД D = 0.9, F = 10^-7. Такой критерий взят из математической статистики и называется критерием Неймана – Пирсона.

Оптимальная фильтрация

Основной операцией при оптимальном обнаружении является вычисление функции взаимной корреляции между принимаемым колебанием u₁(t) ожидаемым сигналом s₁(t):

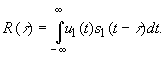
Эта операция выполняется взаимокорреляционным устройством (ВКУ), которое состоит из задерживающего устройства на время τ, умножителя и интегратора (Рис.1)

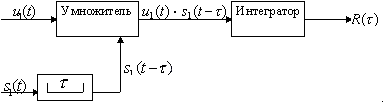
Рис. 1

Это устройство вычисляет для заданного τ одно значение функции взаимной корреляции. Для получения многих значений R(τ) необходимо либо повторить процедуру для различных τ, либо использовать параллельную цепь задерживающих устройств. Если время поступления сигнала известно, то достаточно вычислить лишь R(0), однако чаще всего время прихода является случайной функцией, и поэтому приходится анализировать всю функцию R(τ), принимая решение о наличии сигнала по её максимуму.

Можно построить схему ВКУ в виде простого линейного устройства с постоянными параметрами, на выходе которого получают непрерывную функцию R(τ), а временная задержка сигнала вносит соответствующую задержку в выходной сигнал.

Такое устройство называют линейным фильтром. Связь входного и выходного сигналов в линейном фильтре описывается интегралом свертки

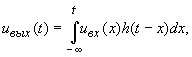
где h(t)- импульсная характеристика фильтра.

Если подобрать линейную цепь так, чтобы напряжение на её выходе с точностью до произвольного множителя k воспроизводило бы взаимокорреляционную функцию (с некоторым запаздыванием t₀), т.е.

то её импульсная характеристика должна удовлетворять равенству

Это может быть проиллюстрировано на следующем примере (см. рис. 2)

Импульсная характеристика является зеркальным отображением сигнала

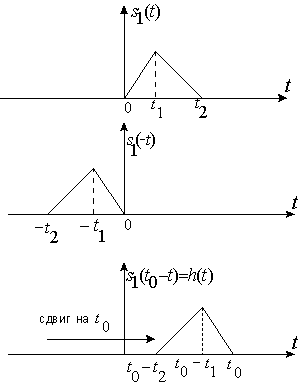
Рис. 2

Линейная система, имеющая такую импульсную характеристику, называется оптимальным фильтром. Она выполняет операцию вычисления взаимной корреляционной функции. Чтобы сигнал на выходе появился после прихода сигнала, должно выполняться условие t₀ > t₂. Оптимальный фильтр является лучшим по критерию получения на выходе максимального отношения сигнал-шум при заданной форме сигнала и интенсивности белого шума на его выходе.

При обнаружении узкополосного радиосигнала

где – медленно меняющиеся огибающая и фаза узкополосного сигнала, импульсная характеристика фильтра должна иметь вид

где звездочка означает комплексно-сопряженную функцию. Если сигналы имеют очень сложную форму или имеют очень большую длительность, то построение оптимальных фильтров для них является очень сложной задачей.