Декартовая система координат в пространстве.
|
|
График 1.2.1.1. Декартова система координат |
Скалярное произведение двух векторов и его свтойства.
Определение скалярного произведения
Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла междуними.
Обозначается ab,а* b(или( а, b)).Итак, по определению,
Формуле (6.1) можно придать иной вид. Так как | a| cosg=пр ba, (см. рис.14), a |b| cosg = пр ab, то получаем:
т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.
Свойства скалярного произведения
1. Скалярное произведение обладает переместительным свойством: ab=ba
Решение:
5. Если векторы а и b (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если a ^b, то ab=0. Справедливо и обратное утверждение: если ab=0 и а¹ 0¹b, то а ^ b
.
Скалярное произведение векторов в координатной форме.
Скалярное произведение в координатах
Если 
то 
Векторное произведение двух векторов и его основные свойства.
Векторное произведение
Векторное
произведение векторов
и 
-
вектор, обозначаемый 
или 
для
когорого:
1) 
(
-
угол между векторами
и
, 
);
2) 
3) тройка , , - правая.
Свойства
векторного произведения:
если 
,
то 
равен
площади параллелограмма, построенного
на приведенных к общему началу
векторах
и
.
Выражение векторного произведения через координаты.
Векторное произведение в координатах
Если
,
то 
или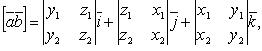 
или 
В
частности 
Смешанное произведение трех векторов и его свойства.
Смешанное
произведение записывают в виде:
.
Смысл смешенного произведения: сначала два вектора векторно перемножают, а
затем полученный скалярно перемножают с третьим вектором. Смешанное
произведение представляет собой число – число. Результат смешанного
произведения – объем параллелепипеда, образованного векторами.
Свойства.
1. Смешанное произведение не меняется при циклической перестановке
сомножителей:
2. Смешанное произведение не изменится при перемене местами векторного и
скалярного произведения.
3. Смешанное произведение меняет знак при перемене мест любых двух
векторов-сомножителей.
4. Смешанное произведение трех ненулевых векторов равно нулю тогда и
только тогда, когда они компланарны.
Три вектора называются компланарными, если результат смешанного произведения
равен нулю.
Выражение смешанного произведения через координаты.
Смешанное произведение в координатах
Если
то
