20. Статические модели надежности по (простая интуитивная модель, модель Нельсона, модель Миллса).

Статические модели отличаются от динамических прежде всего тем, что в них не учитывается время появления ошибок.

МОДЕЛЬ МИЛЛСА. Использование этой модели предполагает необходимость перед началом тестирования искусственно вносить в программу некоторое количество известных ошибок. Ошибки вносятся случайным образом и фиксируются в протоколе искусственных ошибок. Специалист, проводящий тестирование, не знает ни количества, ни характера внесенных ошибок. Предполагается, что все ошибки (как естественные, так и искусственно внесенные) имеют равную вероятность быть найденными в процессе тестирования.

Программа тестируется в течение некоторого времени и собираются статистики об обнаруженных ошибках.

Пусть после тестирования обнаружено n собственных ошибок программы и v искусственно внесенных ошибок. Тогда первоначальное число ошибок в программе N можно оценить по формуле Миллса

где S - количество искусственно внесенных ошибок.

Например, если в программу внесено 50 ошибок и в процессе тестирования обнаружено 25 собственных и 5 внесенных ошибок, то по формуле Миллса делается предположение, что первоначально в программе было 250 ошибок.

Вторая часть модели связана с проверкой гипотезы об N. Допустим, мы считаем, что в программе первоначально К ошибок. Вносим искусственно в программу S ошибок и тестируем ее до тех пор, пока все искусственно внесенные ошибки не будут обнаружены. Пусть при этом обнаружено n собственных ошибок программы. Вероятность, что в программе первоначально было K ошибок, можно рассчитать по соотношению (1):

Например, если утверждается, что в программе нет ошибок (K=0) и при внесении в программу 10 ошибок все они в процессе тестирования обнаружены, но при этом не выявлено ни одной собственной, то

.

Таким образом, с вероятностью 0,91 можно утверждать, что в программе нет ошибок. Но если в процессе тестирования обнаружена хоть одна собственная ошибка, то P = 0.

Формулу (1) можно использовать только в случае, если обнаружены все S искусственно внесенных ошибок. Если же обнаружено только v искусственно внесенных ошибок, то применяют формулу

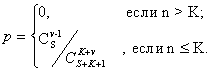
Например, если утверждается, что в программе нет ошибок, а к моменту оценки надежности обнаружено 5 из 10 искусственно внесенных ошибок и не обнаружено ни одной собственной ошибки, то вероятность того, что в программе действительно нет ошибок, будет равна

.

Если при тех же исходных условиях оценка надежности производится в момент, когда обнаружены 8 из 10 искусственных ошибок, то

.

Достоинством модели Миллса является простота применяемого математического аппарата и наглядность.

Однако есть недостатки:

1. необходимость внесения искусственных ошибок (этот процесс плохо формализуем);

2. достаточно вольное допущение величины K, которое основывается исключительно на интуиции и опыте человека, проводящего оценку, т.е. допускает большое влияние субъективного фактора.

ПРОСТАЯ ИНТУИТИВНАЯ МОДЕЛЬ. Использование этой модели предполагает проведение тестирования двумя группами программистов (или двумя программистами в зависимости от величины программы) независимо друг от друга, использующими независимые тестовые наборы. В процессе тестирования каждая из групп фиксируют все найденные ею ошибки.

Пусть первая группа обнаружила n₁ ошибок, вторая n₂, n₁₂ - это число ошибок, обнаруженных как первой, так и второй группой.

Обозначим через N неизвестное количество ошибок, присутствующих в программе до начала тестирования. Тогда можно эффективность тестирования каждой из групп определить как

Эффективность тестирования можно интерпретировать как вероятность того, что ошибка будет обнаружена. Таким образом, можно считать, что первая группа обнаруживает ошибку в программе с вероятностью, вторая - с вероятностью .

Тогда вероятность p₁₂ того, что ошибка будет обнаружена обеими группами, можно принять равной . С другой стороны, так как группы действуют независимо друг от друга, то р₁₂ = р₁р₂. Получаем .

Отсюда получаем оценку первоначального числа ошибок программы : .

МОДЕЛЬ НЕЛЬСОНА. В модели предполагается, что область, которой могут принадлежать входные данные программы, разделена на k непересекающихся областей Z_i, i = 1,2,...,k. Пусть p_i - вероятность того, что для очередного выполнения программы будет выбран набор данных из области Z_i. Значения p_i определяются по статистике входных данных в реальных условиях работы ПО.

Пусть к моменту оценки надежности было выполнено N_i прогонов ПО на наборах данных из области Z_i, и n_i из этих прогонов закончились отказом. Тогда надежность ПО оценивается по формуле .