42. Элементы математической логики. Высказывания и логические связки.

Математическая логика - это анализ методом рассуждений, при этом в первую очередь исследуются формы рассуждений, а не их содержание, т. е. математическая логика, исследует соотношения между основными понятиями математики, на базе которых доказываются математические утверждения. Базовыми элементами, которыми оперирует алгебра логики, являются высказывания. Высказывания строятся над множеством {B,  ,  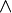,  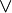, 0, 1}, где B — непустое множество, над элементами которого определены

операции:

Конъюнкция - Логическая операция, ставящая двум элементарным высказываниям новое высказывание, которое истинно только тогда, когда истинно А и В одновременно и ложно во всех остальных случаях. (F=А^В

F=А*В, F=А&В, F=А и В)

Дизъюнкция - Логическая операция, ставящая двум элементарным высказываниям новое, которое истинно тогда, когда истинно либо А, либо В, либо А и В одновременно и ложно только тогда, когда высказывание А и В ложно. (F= АѵВ, F=А+В, F=А ИЛИ В)

Отрицание - Логическая операция, ставящая элементарному высказыванию новое высказывание, которое истинно только тогда, когда исходное высказывание ложно. (F=НЕ, F=¬А, F=Ā,F=~А)

Импликация - Логическое выражение, ставящая двум элементарным высказываниям новое высказывание, которое ложно только тогда, когда А истинно, В ложно. И истина в остальных случаях. (F=А=>В, F=А→В)

Эквивалентность - Логическая операция, ставящая двум эквивалентам новое высказывание, которое истинно или одновременно ложно. И ложно только тогда, когда одно из высказываний А и В ложно, а другое истинно, равносильно. (F=АΞВ, F=А↔В, F=А=В)