3. Второе начало термодинамики. Обратимые и необратимые процессы. Энтропия

2 Начало термодинамики.

Содержание второго начала термодинамики.

Первого начала термодинамики недостаточно для полной характеристики термодинамических процессов. В рамках первого начала можно установить энергетический баланс процессов, но получить сведения о возможности, направлении и пределах их протекания не представляется возможным.

Итак, второе начало позволяет:

• находить направление и устанавливать возможность самопроизвольного (естественного, спонтанного) течения термодинамических процессов и пределы их протекания;

определять условия, при которых превращение какого-либо запаса энергии в полезную работу происходит наиболее полно.

Обратимые и необратимые процессы.

Подобно тому, как в первом начале термодинамики вводится функция состояния – внутренняя энергия, во втором начале – функция состояния, получившая название энтропия (S) (от греческого entropia – поворот, превращение). Рассмотрение изменения этой функции привело к разделению всех процессов на две группы: обратимые и необратимые (самопроизвольные) процессы.

Процесс называется обратимым, если его можно провести сначала в прямом, а затем в обратном направлении и так, что ни в системе, ни в окружающей среде не останется никаких изменений. Полностью обратимый процесс – абстракция, но многие процессы можно вести в таких условиях, чтобы их отклонение от обратимости было весьма мало. Для этого необходи-

мо, чтобы в каждой своей бесконечно малой стадии состояние системы, в которой этот процесс происходит, отвечало бы состоянию равновесия.

Состояние равновесия – особое состояние термодинамической системы, в которое она переходит в результате обратимого или необратимого процессов и может оставаться в нем бесконечно долго. Реальные процессы могут приближаться к обратимым, но для этого они должны совершаться медленно.

Процесс называется необратимым (естественным, спонтанным, самопроизвольным), если он сопровождается рассеянием энергии, т. е. равномерным распределением между всеми телами системы в результате процесса теплопередачи.

В качестве примеров необратимых процессов могут быть названы следующие:

• замерзание переохлажденной жидкости;

• расширение газа в вакуумированное пространство;

• диффузия в газовой фазе или в жидкости.

Систему, в которой произошел необратимый процесс, можно возвратить в исходное состояние, но для этого над системой нужно совершить работу.

К необратимым процессам относится большинство реальных процессов, так как они всегда сопровождаются работой против сил трения, в результате чего происходят бесполезные энергозатраты, сопровождающиеся рассеянием энергии.

Для иллюстрации понятий рассмотрим идеальный газ, находящийся в цилиндре под поршнем. Пусть начальное давление газа Р₁ при его объеме V₁ (рис. 4.1).

Давление газа уравновешено насыпанным на поршень песком. Совокупность равновесных состояний описывается уравнением pV = const и графически изображается плавной кривой (1).

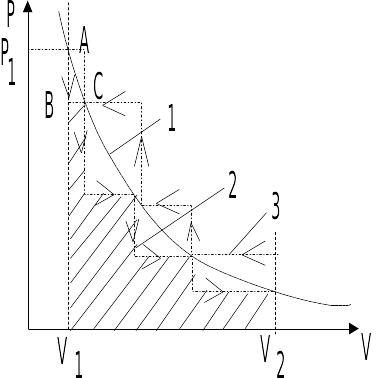
Если с поршня снять некоторое количество песка, то давление газа над поршнем резко снизится (от А до В) лишь после чего произойдет увеличение объема газа до равновесной величины (от В до С). Характер этого процесса – ломанная линия 2. Эта линия характеризует зависимость P=f (V) при необратимом процессе.

Рис. 4.1. Зависимость давления газа от его объема при обратимом (1) и необратимом процессах (2, 3).

Из рисунка видно, что при обратимом расширении газа совершаемая им работа (площадь под плавной кривой 1) больше, чем при любом необратимом его расширении.

Таким образом, любой термодинамический процесс характеризуется максимально возможной величиной работы, если он совершается в обратимом режиме. К аналогичному выводу можно прийти, если рассмотреть процесс сжатия газа. Только следует иметь ввиду, что в этом случае величина работы – отрицательная величина (рис. 4.1, ломаная 3).

Энтропия.

Термодинамическая энтропия — аддитивная термодинамическая величина, функция состояния термодинамической системы.

Энтропия, функция состояния S термодинамической системы, изменение которой dS для бесконечно малого обратимого изменения состояния системы равно отношению количества теплоты полученного системой в этом процессе (или отнятого от системы), к абсолютной температуре

Величина dS является полным дифференциалом, т.е. ее интегрирование по любому произвольно выбранному пути дает разность между значениями энтропии в начальном (А) и конечном (В) состояниях:

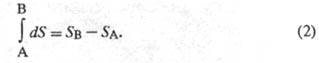
Теплота не является функцией состояния, поэтому интеграл от δQ зависит от выбранного пути перехода между состояниями А и В. Энтропия измеряется в Дж/(моль·град). где р - давление, μi - химический потенциал i-го компонента.

Простые формулы связывают энтропию с теплоемкостями при постоянном давлении Ср и постоянном объеме Cv: С помощью энтропии формулируются условия достижения термодинамического равновесия системы при постоянстве ее внутренней энергии, объема и числа молей i-го компонента (изолированная система) и условие устойчивости такого равновесия: Это означает, что энтропия изолированной системы достигает максимума в состоянии термодинамического равновесия. Самопроизвольные процессы в системе могут протекать только в направлении возрастания энтропии.

Для изолированных систем второй закон утверждает: dS і 0, (4.2) т.е. энтропия изолированных систем в необратимых процессах может только возрастать, а в состоянии термодинамического равновесия она достигает максимума (dS = 0,

d 2S < 0).

При любых процессах, протекающих в термодинамических изолированных системах, энтропия либо остается неизменной, либо увеличивается. Таким образом, энтропия указывает направление самопроизвольно протекающих процессов. Рост энтропии указывает на приближение системы к состоянию термодинамического равновесия. В состоянии равновесия энтропия принимает максимальное значение. Закон возрастания энтропии можно принять в качестве еще одной формулировки второго закона термодинамики.