19. Ограниченная взаимная растворимость жидкостей
Ограниченная взаимная растворимость двух жидкостей имеет место только в тех системах, в которых образование раствора сопровождается поглощением значительного количества теплоты. В этом случае парциальные давления пара обоих компонентов в растворе превосходят парциальные давления пара в соответствующих простейших системах ( положительные отклонения дав-ления пара), что облегчает выделение обоих компонентов из раствора. [1]
Ограниченная взаимная растворимость двух жидкостей наблюдается в системах со значительным отклонением от идеальности. Такая растворимость зависит от температуры, однако влияние температуры на разные системы различно. В одних системах взаимная растворимость жидкостей увеличивается с ростом температуры, и при этом составы двух равновесных жидких фаз сближаются. При некоторой температуре, называемой критической температурой растворения, составы обеих равновесных жидких фаз становятся одинаковыми и достигается полная гомогенность системы. [2]
Ограниченная взаимная растворимость двух жидкостей имеет место только в тех системах, в которых образование раствора сопровождается поглощением значительного количества теплоты. В этом случае парциальные давления пара обоих компонентов в растворе превосходят парциальные давления пара в соответствующих простейших системах ( положительные отклонения давления пара), что облегчает выделение обоих компонентов из раствора. [3]
Ограниченная взаимная растворимость двух жидкостей наблюдается в системах со значительным отклонением от идеальности. Такая растворимость зависит от температуры, однако влияние температуры на разные системы различно. В одних системах взаимная растворимость жидкостей увеличивается с ростом температуры, и при этом составы двух равновесных жидких фаз сближаются. При некоторой температуре, называемой критической температурой растворения, составы обеих равновесных жидких фаз становятся одинаковыми и достигается полная гомогенность системы. [4]
Ограниченная взаимная растворимость двух жидкостей имеет место только в тех системах, в которых образование раствора сопровождается поглощением значительного количества теплоты. В этом случае парциальные давления пара обоих компонентов в растворе превосходят парциальные давления пара в соответствующих простейших системах ( положительные отклонения давления пара), что облегчает испарение обоих компонентов из раствора. [5]
Ограниченная взаимная растворимость или взаимная нерастворимость в жидком состоянии является отнюдь не редким случаем, и даже в металлических системах можно встретить много примеров этого явления. [6]
Ограниченная взаимная растворимость двух жидкостей имеет место только в тех системах, в которых образование раствора сопровождается поглощением значительного количества теплоты. В этом случае парциальные давления пара обоих компонентов в растворе превосходят парциальные давления пара в соответствующих простейших системах ( положительные отклонения давления пара), что облегчает выделение обоих компонентов из раствора. [7]
Ограниченная взаимная растворимость газов возникает при очень высоких давлениях, когда отступления газов от идеальности чрезвычайно велики. Впервые экспериментально расслоение газов наблюдалось в системе азот - аммиак. Такое давление соответствует критическому состоянию. С ростом давления составы равновесных фаз становятся все более различными. С ростом температуры область расслоения уменьшается, хотя состав критических фаз изменяется мало. [8]
Ограниченной взаимной растворимостью в жидком состоянии характеризуются системы галлия с таллием, кадмием, висмутом и свинцом, а также ртутью. При 30 в ртути с образованием амальгамы растворяется только 1 36 вес. [9]
Установлена ограниченная взаимная растворимость газов при высоких давлениях. Так, газовая смесь из аммиака и азота при 148 и давлении 10000 кг / см2 расслаивается на две газовые фазы, из которых одна содержит около 70 % аммиака, а другая-24 % аммиака. [10]
Наблюдается ограниченная взаимная растворимость жидких озона и кислорода при температурах ниже 180 С. [11]
При ограниченной взаимной растворимости двух жидкостей кривые парциальных давлений паров принимают характерную форму. [12]
Коэффициент теплового расширения — величина, характеризующая относительную величину изменения объёма или линейных размеров тела с увеличением температуры на 1 К при постоянном давлении. В соответствии с этим различают:
Коэффициент объёмного теплового расширения
,
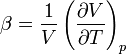К −1 (°C−1) —
относительное изменение объёма тела
при нагревании его на 
градусов
при постоянном давлении,
и, для твёрдых тел,
[править]Коэффициент линейного теплового расширения
Коэффициент линейного теплового расширения показывает относительное изменение длины тела при нагревании на температуру ΔT:
—
относительное
изменение линейного размера тела при
нагревании его на dT
градусов при постоянном давлении.
В общем
случае, коэффициент линейного теплового
расширения может быть различен при
измерении вдоль разных направлений:
αx,
αy,
αz.
Для изотропных тел 
и
αV = 3αL;.
Для определения критической температуры растворения Алексеев предложил использовать приближенное правило прямолинейного диаметра, согласно которому среднее арифметическое из состава равновесных ( жидких) фаз является линейной функцией температуры. Диаграмма температура расслоения - состав позволяет определить как состав системы, так и количественное соотношение фаз в любой точке. [1]
Уравнение ( 6 - 44) выражает собой так называемое правило прямолинейного диаметра. [2]
Если TK определяется визуально и р № рассчитывается на основе закона прямолинейного диаметра, то Рвд получают непосредственно при наблюдаемой темпера туре - Т, или по P-V изотерме. Однако, при более точном определении Рк, то есть до 0 02 МПа должны быть введены поправки на гидростатический и гравитационный эффекты. [3]
Это правило дает возможность установить ( в конденсированной системе) соотношения масс комплексов, о которых говорилось в правиле прямолинейного диаметра. Когда на фазовой диаграмме мы имеем две точки, отвечающие каким-либо комплексам, и третью точку, представляющую средний состав суммы этих комплексов, тогда, согласно правилу рычага, массы обоих комплексов обратно пропорциональны длинам отрезков, на которые точка среднего состава системы делит прямую, которая соединяет точки, соответствующие комплексам. Правило рычага остается, конечно, справедливым, когда измеряются не длины отрезков между указанными точками, а длины их проекций, например, на ось абсцисс. [10]