10. Расчет константы химического равновесия через изобарный потенциал.

Изобарный потенциал системы, в которой химическая реакция протекает неравновесно, изменяется : _i_i  0. Найдем это изменение. Обозначим : P_i  исходные парциальные давления компонентов в неравновесной смеси.

= _i_i ; _i = G_i(T) + RT ln P_i

= _iG_i(T) + RT_i ln P_i

Первый член правой части уравнения (_iG_i(T)) одинаков для всех состояний данной реакции  равновесных и неравновесных. Следовательно, можно подставить его значение из уравнения, приведенного ранее при выводе ЗДМ (см. предыдущую лекцию) :

=  RT ln K_P + RT_i ln P_i

Если смесь компонентов реакции с парциальными давлениями P_i имеет настолько большую массу, что изменение масс компонентов на величины _i практически не изменяет парциальных давлений, то в уравнении можно заменить равной ей величиной . Положив  = 1, получим :

(G)_P,T = =  RT ln K_P + RT_i ln P_i

Это уравнение изотермы химической реакции. Здесь G  изменение изобарного потенциала системы при химическом превращении такого числа молей реагирующих веществ, которое соответствует стехиометрическому уравнению реакции. G называется изобарным потенциалом реакции.

Если исходные парциальные давления всех участников реакции P_i = 1, то

G^о =  RT ln K_P

G^о  стандартный изобарный потенциал реакции.

Аналогично :

= _i_i ; _i = G_i (T) + RT ln C_i

C_i  исходная концентрация реагирующих веществ.

= _iG_i (T) + RT_i ln С_i

В состоянии равновесия :

_i_i = 0 ; _iG_i (T) + RT_i ln с_i = 0

Здесь с_i  равновесная концентрация.

_i ln с_i =  ; _iG_i (T) =  RT ln K_C

=  RT ln K_C + RT_i ln С_i

Аналогично заменяем на ;  = 1 :

(F)_V,T =  RT ln K_C + RT_i ln С_i

F называют изохорным потенциалом химической реакции или свободной энергией химической реакции.

Если исходные концентрации С_i = 1, то

F ^о =  RT ln K_C

F ^о  стандартный изохорный потенциал реакции.

(G)_P,T = (F)_V,T , т.к. каждая из обеих величин равна _i_i .

11. Равновесие в гетерогенных системах. Уравнение Клапейрона — Клаузиуса — 

Большинство веществ могут существовать в одном из трех агрегатных состояний: газообразном (парообразном), жидком и твердом. В определенных условиях эти фазы способны переходить друг в друга, то есть всякую жидкость путем испарения можно перевести в газ, а охлаждением – в твердое состояние. На рис. 6.9 показаны взаимные фазовые превращения вещества.

Рисунок 6.9 Взаимное превращение трех агрегатных состояний друг в друга

Равновесия между различными фазами одной системы называют фазовыми, а описывают эти фазовые равновесия посредством фазовых диаграмм или диаграмм состояния. Фазовая диаграмма позволяет установить условия равновесия между числом фаз, числом компонентов и числом степеней свободы (вариантностью) системы.

Фаза (Ф) – гомогенная (однородная по химическому составу и термодинамическим свойствам) часть системы, отделенная от других частей поверхностью раздела. Так, два нерастворимых друг в друге твердых вещества, как и две несмешивающиеся жидкости, образуют две фазы.

Компоненты (К) – химически индивидуальные вещества, наименьшее число которых достаточно для образования фаз системы.

Число компонентов определяется количеством индивидуальных веществ в системе за вычетом числа возможных между ними обратимых взаимодействий. Например, система из трех индивидуальных веществ H₂O, H₂, O₂ будет двухкомпонентной, поскольку для образования всех фаз достаточно любых двух веществ: 

= H2 + 1/2O2.

По числу компонентов системы делятся на одно-, двух-, трех- и многокомпонентные.

Степени свободы (С) – число параметров (температура, давление, состав системы), которые можно произвольно менять без изменения числа фаз в системе.

Правило фаз Гиббса: в изолированной равновесной системе число степеней свободы равно числу компонентов системы плюс два минус число фаз: 

С = К + 2 – Ф

В качестве примера однокомпонентной системы, для которой правило фаз С = 3 – Ф, на рис. 6.10 приведена фазовая диаграмма диоксида углерода.

Рисунок 6.10 Фазовая диаграмма CO2

При P < 5,3 атм. CO₂ в жидком состоянии не может находится. При атмосферном давлении твердый диоксид углерода сублимирует при 195 K.

Если один из параметров системы (температура или давление) имеет постоянное значение, то правило фаз принимает вид: 

C = K + 1 – Ф.

Это уравнение используется при изучении конденсированных систем, состоящих только из твердых и жидких фаз, поскольку состояния равновесия в таких системах малочувствительны к изменению давления.

Уравнение Клапейрона — Клаузиуса — термодинамическое уравнение, относящееся к квазистатическим (равновесным) процессам перехода вещества из одной фазы в другую (испарение, плавление, сублимация, полиморфное превращение и др.). Согласно уравнению, теплота фазового перехода (например, теплота испарения, теплота плавления) при квазистатическом процессе определяется выражением

где   — удельная теплота фазового перехода,   — изменение удельного объёма тела при фазовом переходе.

Уравнение названо в честь его авторов, Рудольфа Клаузиуса и Бенуа Клапейрона.

Между температурой фазового перехода и внешним давлением существует функциональная связь, причём при фазовом переходе производная 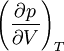  терпит разрыв. Тогда изотермы для рассматриваемого вещества будут иметь характерный вид, изображённый на рисунке. Для вывода существенен горизонтальный участок изотермы, соответствующий фазовому переходу. Слева и справа от этого участка всё вещество находится в одной фазе. Осуществим цикл Карно при бесконечно малой разности температур следующим образом: сначала сообщаем телу теплоту, переводя его из состояния 1 в состояние 2, затем адиабатически охлаждаем его на температуру dT, после чего замыкаем цикл, отводя теплоту и переводя вещество в фазу 1 с последующим адиабатическим нагревом. Совершённая работа равна площади цикла:

Сообщённая теплота равна

где   — удельная теплота фазового перехода,   — масса тела. Согласно теореме Карно,

Отсюда

12. интегрирование уравнения клапейрона-клаузиуса

Поскольку теплота парообразования положительна, а мольный объем пара больше мольного объема конденсированной фазы, это значит, что производная в уравнении Клапейрона-Клаузиуса  т.е. с ростом температуры давление насыщенного пара увеличивается.

При температурах, далеких от критических, мольный объем пара много больше мольного объема конденсированной фазы, поэтому последним можно пренебречь, а если в этой области температур насыщенный пар подчиняется уравнению состояния идеального газа, то:  , и уравнение Клапейрона-Клаузиусаможно представить в виде:  .

В нешироком интервале температур теплоту испарения можно считать постоянной и взятие определенного интеграла дает:  .

Таким образом, если известна ∆v H, то, зная давление насыщенного пара вещества при одной температуре, можно рассчитать давление насыщенного пара при другой температуре. С другой стороны, определив давление насыщенного пара при двух (по крайней мере) температурах, можно рассчитать теплоту испарения.

Взятие неопределенного интеграла дает (при ∆v H = const)  или  , где А и В – константы, характерные для данного вещества. Это уравнение, линейное в координатах ln p – 1/T, дает прямую линию в значительном интервале температур. Более точным является уравнение Антуана:

, где А, В, С – константы.

Практически полезным может оказаться правило Трутона

: энтропия испарения вещества в нормальной точке кипения (при 1 атм.) равна приблизительно 90 Дж/моль*К. Тогда в уравнение Клапейрона-Клаузиуса входит только одна константа Тнтк – температура нормальной точки кипения:

.

По этому уравнению удобно рассчитывать температуру перегонки органических соединений под пониженным давлением. Однако следует отметить, что правило Трутона соблюдается только для «нормальных» жидкостей, т.е. таких молекулы которых не ассоциированы в жидкой фазе (как у воды за счет водородных связей), а также, если пары не состоят из полимерных или диссоциированных молекул.

Для уксусной кислоты прямые определения теплоты испарения в калориметре при температуре кипения СН3СООН равной 391К дает величину 406 Дж/г. С другой стороны при 363 К давление пара 293 торр, при 391К и 760 торр. Заменив производную в уравнении Клапейрона-Клаузиуса отношением конечных приращений имеем:

.

Мольная масса СН3СООН равна 60, тогда из калориметрических данных:

Яндекс.ДиректВсе объявленияВесы торговые Продажа и сервис весов CAS, DIGI, Bizerba, Metler Toledo, Штрих-М, Масса-Кits74.ru 

.

Расхождение между этими двумя значениями связано с тем, что для получения одного моля пара необходимо испарить больше, чем 60 г СН3СООН, следовательно, мольная масса пара СН3СООН равна:

, отсюда легко сообразить, что пары уксусной кислоты в этом температурном интервале димеризованы примерно на 2/3.

Насыщенный пар обладает еще рядом интересных свойств. Рассмотрим некоторые из них.

Пусть в гетерогенной системе при температуре Т находится 1 моль вещества, причем в равновесии находятся m молей пара и 1-m молей жидкой фазы. Пусть теплоемкость пара Сп, жидкости Сж, изменяем температуру от Т до T+dT, при этом испаряется масса жидкости dm, тогда затраты тепла dQ можно представить в виде соотношения:

.

Разделим правую и левую части на Т, имеем:

.

Следовательно, справедливо:  ,

после дифференцирования имеем  .

По уравнению Кирхгоффа   и  ,

т.е. теплоемкость насыщенного пара не равна изобарной теплоемкости того же газообразного вещества.

Следует также иметь в виду, что введение постороннего (инертного) газа изменяет давление насыщенного пара при неизменной температуре, даже если газ не растворяется в жидкости. Это происходит вследствие влияния общего давления на свойства конденсированной фазы (возрастает ее мольная энергия Гиббса). Действительно, при T=const:

, где Рг – давление постороннего газа, Рж давление насыщенного пара, Vж и Vп - мольные объемы жидкости и пара. Поскольку по условию равновесия dGж =dGп, то:  .

Взятие интеграла от Рг = 0 до Рг приводит к уравнению: 

Поскольку дробь Vж/Vn невелика (для воды при 373 К она равна 5,9∙10-4), то влияние постороннего газа сказывается только при высоких давлениях.

Например, для воды под давлением водорода при 373 К

14 Двухкомпонентный жидкий раствор. Закон Рауля. Отклонение от идеальности. Активность, коэффициент

Активность и коэффици­ент активности.

При рассмотрении термодинамических свойств растворов принято пользоваться

отношением

Эта величина называется активностью i в растворе. Согласно уравнению

отношение равно

мольной концентрации данного компонента в растворе. Активность пред­ставляет

собой вспомогательную расчетную термодинамическую функцию, которая

характеризует степень свя­занности молекул компонента. При образовании данным

компо­нентом в растворе каких-нибудь соединений его активность становится

меньше и, наоборот, активность возрастает при уменьшении степени ассоциации

компонента. Активность дает возможность су­дить об отклонении свойств данного

компонента в том или ином растворе от свойств в простейшем растворе при той же

мольной концентрации компонента. Активность зависит от вида и концен­трации

каждого из других компонентов .раствора. Она зависит также от температуры и от

давления, но не зависит от способа выражения концентрации. Химический потенциал

данного компонента в растворе связы­вается с активностью соотношением:

Вместо активности нередко пользуются величиной коэффи­циента активности, g. Он

равен отношению активности к концен­трации g=

. Коэффициент активности характеризует степень отклонения свойств

рассматри­ваемого компонента в данном растворе от его свойств в соответствующем

простейшем растворе. В сильно разбавленном растворе коэффициент активности

равен единице. Чем более концентрирован раствор, тем больше отличается

активность от концентрации.