2.4 Определение запаса прочности и опасного сечения лопатки.
Для оценки работоспособности надо найти минимальный запас прочности лопатки. Для этого необходимо построить график запасов прочности лопатки n по сечениям:
. (1.22)
Где σдл-предел длительной прочности материала (напряжение, вызывающее разрушение лопатки при данной температуре и длительности работы).
Для определения σдл необходимо знать распределение температуры по длине лопатки.
Считаем, что на периферии температура лопатки t п.в. равна температуре газа, заторможенного по относительной скорости на входе в лопатку:
.
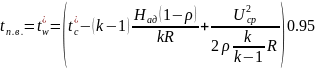(1.23)
Вследствие отвода тепла от лопатки в диск температура лопатки на 1/3 её длины от корня будет переменна по длине и ниже температуры газа на величину
.
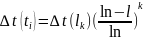(1.24)
Где k - показатель степени: k = 3-5;
l - текущая длина лопатки;
ln - полная длина лопатки;
lk = 0 - длина лопатки в корневом сечении;
Следовательно, температура в i-ом сечении лопатки будет:
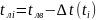. (1.25)
Для каждого сечения лопатки по справочнику находим σдл в зависимости от материала и температуры в данном сечении. Результаты расчёта по формулам записываем в Таблицу 1.7.
Таблица 1.7
Номер сечения |
tлi С °с |
σдл
|
σΣmax H/м2
|
n |
1 |
320 |
280 |
0 |
- |
2 |
300 |
300 |
1.234 |
0.211 |
3 |
290 |
370 |
2.094 |
0.134 |
Cтроим графики tл=f(l), n=f(l).
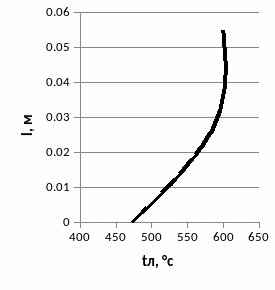
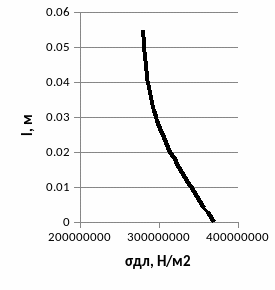
Рис. 1.8. Графики зависимости tл=f(l), n=f(l).
Запас прочности увеличивается от корня к концу лопатки.
Расчёт частоты колебания лопатки
L - длина лопатки.
Rk – радиус расположения корневого сечения.
ω – Угловая скорость вращения рабочего колеса.
ρ – плотность материала лопатки.
Nc – число поперечных сечений с заданной геометрической характеристикой.
F(i), где i = 1… Nc – массив площадей поперечных сечений.
J(i) – массив минимальных моментов инерции поперечных сечений (сечения в которых задаются геометрические характеристики делят лопатку на равные по длине участки; изменение характеристик в приделах каждого участка происходит по линейному закону)
Nm – число сосредоточенных масс дискретной модели упруго-инерционной системы лопатки, создаваемой на основании введённых данных (крыло лопатки с заданной геометрией делится на Nm элементов равной длины; для каждого элемента рассчитывается масса; масса каждого элемента представляется дискретной точечной массой в сечении, расположенном посреди элемента; участки, расположенные между корневым сечением и сечениями с дискретными массами полагаются безынерционными стержнями постоянного поперечного сечения, геометрические характеристики которых определяются, как среднее значение характеристик граничных сечений при расчёте деформации стержневых элементов дискретной модели принимается во внимание только изгибная деформация).
Геометрические характеристики i-ого сечения лопатки.
i |
1 |
2 |
3 |
Zi |
0 |
0.0275 |
0.055 |
Fi |
1.129·10-5 |
0.736·10-5 |
0.431·10-6 |
Ii |
1.856·10-6 |
1.528·10-16 |
0.0871·10-6 |
.
.
= 4500
Em = 0.11·105 Мпа
Результаты расчёта.
Дискретная модель: Nm=5; M= 4.836·10-3; ω = 1355 рад/с
i |
1 |
2 |
3 |
4 |
5 |
6 |
M(i)/M |
0.3308 |
0.2518 |
0.1833 |
0.1357 |
0.0985 |
0 |
L(i)/DL |
0.1 |
0.3 |
0.5 |
0.7 |
0.9 |
1 |
Частота f, Гц |
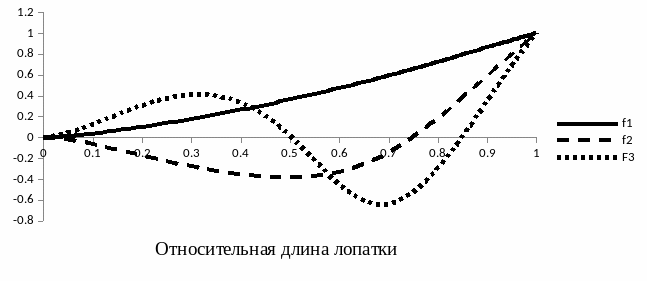
Форма колебаний |
|||||
Y(1) |
Y(2) |
Y(3) |
Y(4) |
Y(5) |
Y(6) |
|
332.2 |
0.0655 |
0.2398 |
0.4291 |
0.6376 |
0.8597 |
1 |
790.7 |
-0.089 |
-0.3125 |
-0.4363 |
-0.2261 |
0.5742 |
1 |
1353 |
0.1995 |
0.6335 |
0.3665 |
-0.7746 |
0.3132 |
1 |
Оглавление