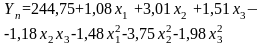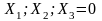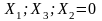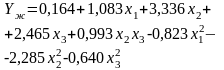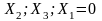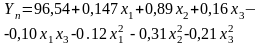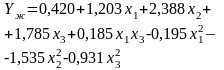6.4. Вариант задания
По условию задачи (таблица 6.2) для математической модели процесса (объекта), выбранной в соответствии с вариантом задания (табл. 6.4), который определяется суммой двух последних цифр номера зачетной книжки студента, построить двухмерные сечения поверхностей отклика.
Таблица 6.4 - Варианты задания
№ |
Вид материала |
Параметр оптимизации |
Уравнение регрессии |
Факторы |
1 |
Трикотажное полотно арт. 271304 |
Прочность |
|
|
2 |
|
|||
3 |
Жесткость |
|
|
|
4 |
|
|||
5 |
|
|||
6 |
Искусственная кожа арт.023 |
Прочность |
|
|
7 |
|
|||
8 |
|
|||
9 |
Жесткость |
|
|
|
10 |
|
|||
11 |
|
6.5. Содержание отчета по работе
1. Интервалы и уровни варьирования факторов для заданного варианта (табл. 6.2), уравнение регрессии.
2. Расчет координат нового центра и угла поворота осей координат в новом центре.
3. Уравнение регрессии в канонической форме.
4. Характеристика вида поверхности отклика.
5. Расчет данных для построения контурных кривых поверхности отклика, представленный в виде табл. 6.3.
6. Рисунок с сечениями поверхности отклика.
7. Выводы по работе.
Контрольные вопросы
1. С какой целью выполняется каноническое преобразование уравнений?
2. В чем заключается каноническое преобразование уравнений второй степени?
3. Как определяют положение нового центра в старых осях координат?
4. Как производится поворот осей координат?
5. Как определяют вид поверхности отклика?
6. Какова последовательность построения двухмерных сечений?
7. Какую информацию дает анализ семейства кривых?