1. Метод покоординатного спуска или Метод Гаусса – Зейделя

min F(X);

X₀€XП

Минимум целевой функции в области протяжения.

Х₀ – начальная точка поиска.

В методе Гаусса – Зейделя поиск совершают в направлении координатных осей.

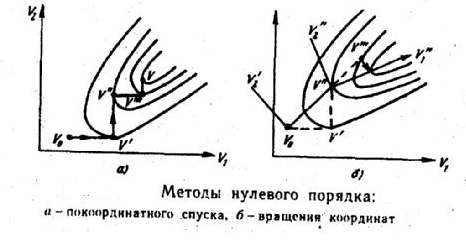
h_нач – начальная величина шага поиска.

Для поиска минимума используются методы одномерной оптимизации.

Метод случайного поиска

Направление поиска выбирается случайно, путём выбора n случайных чисел, равномерно распределённых на отрезке [-1;1) из генератора случайных чисел, который есть в каждой ЭВМ.

n – число управляемых параметров.

Метод градиента

grad F(X) = (∂F/∂x₁; ∂F/∂x₂; …; ∂F/∂x_n)

F(x₁; x₂)

Производные вычисляются численно, путём приращения управляемых параметров.

x₁ = x_1,0 + ∆x₁

∂F/ ∂x₁ = ∆F/∆x₁ ; ∆F = F(x₁₀ + ∆x₁) – F(x₁₀)

В каждой точке для нахождения производных необходимо n+1 вычислений F(X).

Метод наискорейшего спуска

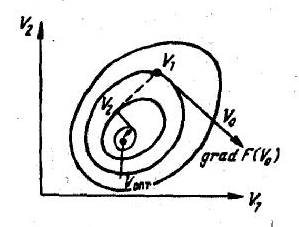
Метод Ньютона

В основу метода положен одноимённый метод решения нелинейных алгебраических уравнений.

grad F(X) = 0;

Обозначим Ф(X) = ∂F(x)/∂x = 0

Применим к данной системе уравнений метод Ньютона.

Ф(X_k) + ∂F(X_k)/∂X ∆X ≈0,

где ∆Х – значение X_k+1 - X_k

X_k+1 = X_k – (∂Ф/∂X)^-1 * Ф(X_k)

X _k+1 = X_k – Ю_k^-1 grad F(X_k) - Формула Ньютона.

Если целевая функция является квадратичным многочленом по управляемым параметрам, то минимум находится за один шаг.

Недостатки метода:

1. Высокая трудоёмкость вычисления и обращения матрицы Гессе.

2. Не всегда имеет место сходимость решения.

Методы одномерного поиска

Найти минимум целевой функции: min F(X_k + hg) = min f(h)

^h>0

g – единичный вектор выбранного направления.

Метод половинного деления (бисекции)

Метод золотого сечения

Золотое сечение – это деление отрезка АВ на 2 части таким образом, что большая его часть АС является средней пропорциональной между отрезком АВ и его меньшей частью СВ.

АВ/АС = АС/СВ

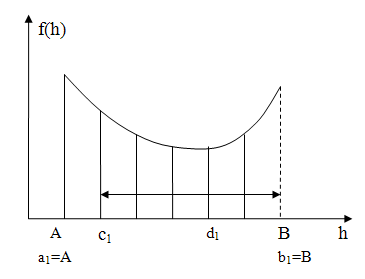
Для шага а_к и в_к

c_к = а_к + 0,382l_k

d_k = в_к – 0,382 l_k

l_k = b_k - a_k

Если f(c_k) < f(d_k), то b_k+1 = d_k; d_k+1 = c_k; a_k+1 = a_k;

Если f(c_k) ≥ f(d_k), то a_k+1 = c_k; c_k+1 = d_k; b_k+1 = b_k

Если l_k ≤ ε – условие окончания операции.

В методе золотого сечения для сужения интервала неопределённости необходимо сделать только одно вычисление.

Метод чисел Фибоначчи

β_k = β_k-1 + β_k-2 , где β₂ = β₁ , β_k = 1,1,2,3,5,8,13,21,34,55,89…

k = 0,1,2,3,4,5, 6, 7, 8, 9, 10,…

ε ≈ В-А / 1,618^N ,

где N – число итераций (число последовательных вычислений). N задаётся.

Определяется порядковый номер числа Фибоначчи К = N + 2

Это – максимальный номер числа Фибоначчи- К.

с_n = a_n +α_nl_n ; α_n = β_N+2-n / β_N+3-n ;

d_n = b_n- α_nl_n.

Метод полиноминальной аппроксимации

f (h) = a₀ + a₁h + a₂h² h` = a₁/2a₂

h` = h_c + (h[f(h_a) – f(h_b)]) / (2[f(h_a) – 2f(h_c) + f(h_b)])

h_a = h_c – H₁

h_b = h_c + H₁

Сведение задач условной оптимизации к безусловной

Для сведения задач условной оптимизации к безусловной используют метод штрафных функций.

Метод внешней точки

Например, имеем ограничения типа неравенств φ(X) < 0

Ф(Х) = F(X) + Q_k(X)

Q_k(X) = r_k ∑ [max {0; φ_i(X)}] ²; r_k > 0 – функция штрафа в методе внешней точки.

Решаем задачу. Найти минимум целевой функции при выполнении ограничений - min F(X)

ХД = {X| φ(X) < 0}

Ищем минимум новой функции

min Ф(Х)

Поиск начинают с небольших значений r_k, постепенно его увеличивая до тех пор, пока разница между предыдущим и последующим значением не станет меньше заданной погрешности δ.

ΔХ = Х_k+1 – Х_k < δ.

Метод барьерных функций или метод внутренней точки

Ф(Х) = F(X) – r_k ∑ 1/φ_i(X)

Где функция штрафа имеет вид: Q_k(X) = -r_k ∑ 1/φ_i(X)