Раздел № 3 Методы оптимизации технических объектов

Оптимизация – создание лучших объектов.

Виды описания проектируемых объектов и классификация их параметров

Математическая модель объекта (ММО) – это система математических объектов (чисел, переменных, матриц) и отношений между ними, выражающихся в уравнениях, неравенствах и т.п., описывающих свойства технического объекта.

Среди свойств объекта различают свойства системы, элементов системы и внешней среды. Соответственно они находят своё количественное выражение в выходных , внешних и внутренних параметрах объекта.

Внутренние параметры – параметры электрической системы.

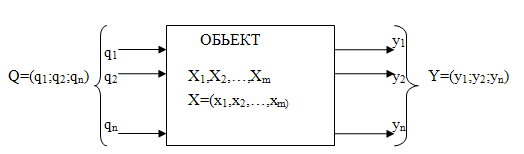
Y = F(X; Q)

F = (f₁; f₂;…; f_n)

y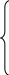 ₁ = f₁(x₁, x₂,…, x_n; q₁, q₂,…,q_n)

y₂ = f₂(X; Q)

………………………………….

y_n = f_n (X; Q)

Переменные, описывающие состояние объекта, называют фазовыми переменными.

Уравнение для фазовых переменных: φ(z, z’,z’’,…,zⁿ) = V,

Большинство выходных параметров являются функционалами, т.е. для их определения необходимо при заданных X и Q решать систему уравнений и по полученным величинам вычислить выходные параметры Y.

Техническое задание включает в себя технические требования к выходным параметрам. Вся совокупность технических требований образует вектор технических требований (Т.Т.)

Он включает в себя:

ТТ = (ТТ₁; ТТ₂;…; ТТ_n)

Соотношение между соответствующими выходными параметрами и техническими требованиями называют условиями работоспособности.

y_i < TТ_i

y_i > TТ_j

TT`_k < y_k < TT"_k

Требования к математическим моделям.

1. Универсальность – характеризует полноту отображения в модели свойств реального объекта.

2. Точность – характеризует степень совпадения параметров реального объекта и их расчётных значений по математической модели.

y_{j мат. мод.} - y_j

ε = у_j ; ε = (ε₁; ε₂;…; ε_n)

ε – относительная погрешность.

ε_max = ||ε|| = max ε_j;

| |ε|| =√ ε₁²+ ε₂²+…+ ε_n²

3. Адекватность - это способность математических моделей отображать заданные свойства объекта, с погрешностью не выше требуемой.

Адекватность модели, как правило, имеет место в ограниченной области изменения внешних и внутренних параметров, называемой областью адекватности (ОА)

Область адекватности – множество значений, внешних и внутренних параметров, для которых погрешность вычисления выходных параметров не превосходит заданную величину δ>0.

ОА = {Q; X}; ε_max ≤ δ

4. Экономичность математической модели – характеризуется затратами вычислительных ресурсов ЭВМ на её реализацию.

Часто экономичность оценивают по порядку системы уравнений или количеству арифметических операций, необходимых для решения - эти оценки не зависят от типа ЭВМ.

Требования высокой точности, универсальности и широкой области адекватности противоречат требованию экономичности. В каждом конкретном случае приходится выбирать оптимальное, компромиссное решение. Поэтому в системах автоматизированного проектирования (САПР) используются модели различных степеней точности, универсальности, адекватности и экономичности.

Основные определения

Критерий оптимальности – это правило, согласно которому выбирается наилучший вариант из некоторого множества.

Будем рассматривать объекты, имеющие неизменную структуру и различающиеся численными значениями внутренних и внешних параметров. В основе построения правильного предпочтения лежит целевая функция, -качества»

F(X); (X€X0)

X = (X₁, X₂,…X_n) – вектор управляемых параметров.

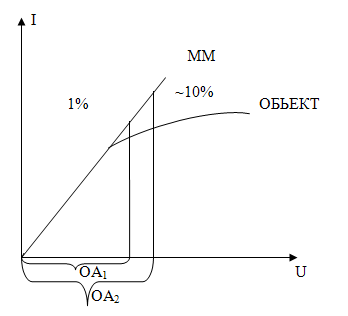
Если значение целевой функции тем больше, чем выше качество объекта, то оптимизация есть максимизация целевой функции

max F(X); X€X0

В противном случае оптимизация есть минимизация целевой функции.

min F(X);

Если область определения Х0 есть дискретное множество точек, то объект – дискретный и имеет задачу дискретного ( в частном случае) целочисленного программирования. В противном случае – это задача параметрической оптимизации непрерывных объектов.

Переход от задачи максимизации к задаче минимизации и наоборот осуществляются сменой знака целевой функции.

Безусловные экстремумы

ε – окрестностью некоторой точки Х₀ будем называть множество точек S_ε(X₀), которые находятся от Х₀ на расстоянии не превышающем заданное число ε > 0.

S_ε(X₀) = {X| ||X – X₀|| ≤ ε}

||X – X₀|| - Норма вектора, отождествляемая с расстояния между точками Х и Х₀

Максимумом целевой функции F(X) называют её значение F(X`), если существует число ε > 0 такое, что для любой точки Х€ S<sub>ε</sub>(Х`) за исключением самой точки Х`.

Выполняется неравенство F(X) – F(X`) < 0 – условие максимума.

Аналогично минимумом функции F(X) называют её значение F(X`), если выполняется условие:

F(X) – F(X`) >0.

Точку Х` называют экстремальной точкой. В точке глобального экстремума максимизируемая (минимизируемая) целевая функция имеет наибольшее (наименьшее) значение среди всех локальных экстремумов.

Задачи, в которых отсутствуют ограничения на области управляемых параметров, относятся к задачам безусловной оптимизации.

Условные экстремумы

При наличии ограничений на область изменения управляемых параметров имеем задачу условной оптимизации.

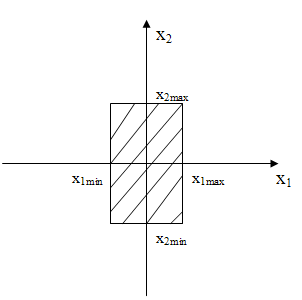
1. Прямые ограничения Х_i > X_{i min} ; Xj< X_{j max} и т.д.

Область допустимых параметров ХД = { X € X₀ | X_i > X_{i min}; X_j < X_jmax} при наличии прямых ограничений.

2. Функциональные ограничения - имеют вид неравенств (равенств)

а) ограничения-неравенства φ(Х)>0, φ=( φ₁, φ₂,…, φ_n)

б) ограничения-равенства Ψ(Х)=0, Ψ=( Ψ₁, Ψ₂,…, Ψ_n)

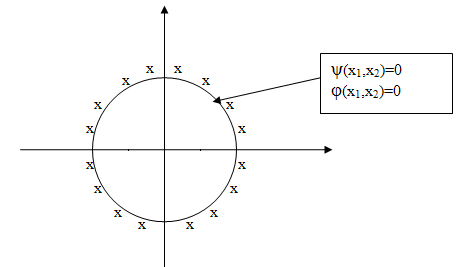
В задачах проектирования роль ограничения часто выполняют условия работоспособности.

XP={X€XД | φ(x) > 0; ψ(x) = 0}

Необходимые и достаточные условия экстремума

В классическом методе используется безусловная оптимизация, когда известно аналитическое выражение целевой функции F(X) и она не менее чем дважды дифференцируема по управляемым параметрам.

Разложим F(X) в ряд Тейлора в окрестности экстремальной точки Х`.

F(X) = F(X`) + ∂F/∂x₁∆x₁ + ∂F/∂x₂ ∆x₂ + … + ∂F/∂x_n ∆x_n + ½! (∂²F/∂x₁²∆x²₁ +

+∂²F/∂x₁∂x₂ ∆x₁∆x₂+ … + ∂²F/∂x_n² ∆x_n²) +... ,

где ∆x_i = x_i -x_i`

∂F/∂x_k – первая производная по x_k.

X₁ – X₁`

∆Х = Х – Х` = X<sub>2</sub> – X<sub>2</sub>` - вектор столбец.

X₃ – X₃`

∆X^t – матрица строка (X₁ – X₁`; X<sub>2</sub> – X<sub>2</sub>`;…; X_n – X_n`)

∂²F/∂x₁²; ∂²F/∂x₁∂x₂; ….∂²F/∂x₁∂x_n

∂²F/∂x₁∂x₂; ∂²F/∂x₂²;……. ∂²F/∂x₂∂x_n

∂²F/∂X²=Ю= …………………………………………. – матрица Гессе.

∂²F/∂x₁∂x_n; ∂²F/∂x₂∂x_n;… ∂²F/∂x_n²

F(X) = F(X`) + ∂F/∂X*∆X + 1/2 ∆X^t * ∂²F/∂X² *∆X + …

F(X) – F(X`) < 0 – условие максимума.

Может выполняться только при ∂F/∂X = grad F = 0 – необходимое условие экстремума.

Точки, в которых выполняется необходимое условие экстремума называются стационарными.

∆X^t * ∂²F/∂X² *∆X < 0

Матрица Гессе Ю, удовлетворяющую данному условию при любых ∆Х называют отрицательно определенной матрицей.

Следовательно, отрицательная определённость матрицы Гессе является достаточным условием максимума.

∆X^t * ∂²F/∂X² *∆X > 0

Соответственно матрицу Гессе, удовлетворяющую данному условию, называют положительно определённой.

Положительно определённая матрица Гессе достаточное условие min.

Седловая точка – это точка, в которой достаточные условия не выполняются, т.е. нет не максимума, не минимума.

Метод неопределённых множителей Лагранжа

Применяется для нахождения условного максимума при известных аналитических выражениях целевой функции и ограничений.

Рассмотрим случай ограничений типа равенств.

Запишем функцию Лагранжа:

Ф(Х; Λ) = F(X) + Λ * Ψ(Х) = F(X) + ∑λ_kψ_k(X), где Λ – Вектор неопределённых множителей Лагранжа.

Если Х€ ХД

то выполняются ограничения и

Ψ(Х) = 0

^{Х € ХД}

Ф(Х; Λ) = F(X)

Х€ ХД

Найдем максимум Ф(Х; Λ):

_p

∂Ф(Х; Λ)/∂Х = ∂F(X)/∂X + ∑ λ_k ^∂Ψ^k(X)

^{k=1 ∂X}

∂Ф(Х; Λ)/∂ Λ = Ψ(Х) = 0.

Метод неопределённых множителей Лагранжа может быть распространён и на задачи с ограничениями типа неравенств.