Экзаменационные вопросы по математике / Шпоры по математике

28) Знакопеременные ряды. Абсолютная сходимость. Знакочередующиеся ряды. Признак сходимости Лейбница.

Числовые ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными рядами.

Числовой ряд вида u1-u2+u3-u4+…+ +(-1)n-1.un+…, где un – модуль члена ряда, называется знакочередующимся числовым рядом.

Если сходится и сам знакопеременный ряд и ряд, составленный из абсолютных величин его членов, то говорят, что знакопеременный ряд сходится абсолютно.

Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин членов этого ряда, расходится, то говорят, что знакопеременный ряд сходится условно.

Признак Лейбница Если для знакочередующегося числового ряда

u1 − u2 + u3 − u4 + ... + (−1)n−1. un + ...

(19) Выполняются два условия:

Члены ряда убывают по модулю u1>u2>…>un>…,

lim un = 0,

n→∞

то ряд (19) сходится, причём его сумма положительна и не превосходит первого члена ряда.

Доказательство. Рассмотрим частичную сумму чётного числа членов ряда S2n=(u1-u2)+(u3-u4)+…+(u2n-1-u2n). По условию u1>u2>…>u2n-1>u2n, то есть все разности в скобках положительны, следовательно, S2n возрастает с возрастанием n и S2n>0 при любом n.

С другой стороны S2n=u1-[(u2-u3)+(u4-u5)+…+(u2n-2- u2n-1)+u2n]. Выражение в квадратных скобках положительно и S2n>0, поэтому S2n<u1 для любого n. Таким образом, последовательность частичных сумм S2n возрастает и ограничена, следовательно,

lim

существует конечный n→∞ S2n=S. При этом 0<S≤u1. Рассмотрим теперь частичную сумму нечётного числа членов ряда S2n+1=S2n+u2n+1. Перейдём в последнем

lim lim

равенстве к пределу при n→∞: n→∞ S2n+1= n→∞ S2n+

lim

n→∞ u2n+1=S+0=S. Таким образом, частичные суммы как чётного, так и нечётного числа членов ряда имеют

lim

один и тот же предел S, поэтому n→∞ Sn=S, то есть данный ряд сходится. Теорема доказана.

Замечания.

1.Теорема Лейбница справедлива и если условие un>un+1 выполняется, начиная с некоторого номера N.

2.Условие un>un+1 не является необходимым. Ряд

может сходиться, если оно не выполняется.

29) Интегральный признак Коши сходимости числового ряда с неотрицательными членами.

Пусть члены знакоположительного числового ряда u1+u2+…+un… (7) не возрастают: u1³u2≥…≥un≥… и пусть f(x) такая положительная, непрерывная, невозрастающая на промежутке [1;∞) функция, что f(1)=u1, f(2)= u2 ,…, f(n)= =un,… . Тогда ряд (7)

Соотношение (17) принимает вид: Sn<u1+Y при любом n. Это означает, что последовательность частичных сумм Sn ряда (7) ограничена и, следовательно, ряд (7)

∞

ò f (x)dx

последовательность частичных сумм Sn ряда (7) неограничена и, следовательно, ряд (7) расходится. Теорема доказана.

30) Функциональные ряды. Их основные свойства, связанные с понятием равномерной сходимости (б/д).

Рассмотрим последовательность функций, определенную на множестве Х: { fn (x)}, x Î X .

последовательность.

Равномерная сходимость функциональных рядов.

Для функциональных рядов рассматривается еще один вид сходимости − равномерная сходимость. Определение. Функциональный ряд называется равномерно сходящимся в некоторой области Х, если

для любого сколь угодно малого числа 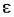> 0 можно указать такое целое число N() > 0, зависящее только от e и не зависящее от х, что при всех n > N()

неравенство выполняется для всех х из области Х.

Свойства равномерно сходящихся рядов.

1.Сумма S(x) равномерно сходящегося ряда

в области Х, где un(x) (n = 1, 2, 3, …) - непрерывные функции, является непрерывной функцией в области Х.

2. Равномерно сходящийся ряд , где un(x) (n = 1, 2, 3, …) -непрерывные функции, можно почленно интегрировать, т.е. справедливо равенство

. (26)

3. Если ряд

,

составленный из функций, имеющих непрерывные

производные , сходится в области C и его сумма равна S(x), а ряд из

производных сходится в этой области

равномерно, то производная суммы ряда равна сумме ряда из производных:

. (27)

Коротко эту теорему формулируют так:

Если ряд, составленный из производных сходящегося ряда (27), сходится равномерно, то исходный ряд (24) можно почленно дифференцировать.

31) Критерий равномерной сходимости функционального ряда.

Определение. Пусть функции fn (x) и f (x) определены на множестве Х. Говорят, что

функциональная последовательность { fn (x)}

равномерно сходится к функции f (x) на множестве

Х, если для любого ε > 0 существует число N (ε) , не зависящее от х, такое, что для всякого натурального n > N (ε) и любого x X выполняется

неравенство fn (x) − f (x) < ε .

Можно также определить равномерную сходимость не в терминах сходимости последовательности частичных сумм, а в терминах остатков ряда.

Определение. Сходящийся в области X функциональный ряд (12) называется равномерно

x X .

32) Критерий Коши равномерной сходимости функционального ряда

Критерий Коши.) Для того, чтобы функциональный ряд

∞

åun (x) сходился равномерно в области X , n=1

необходимо и достаточно , чтобы для любого ε > 0

un+1(x) +un+2 (x) + +un+p (x) <ε

выполняется сразу для всех x X .

На практике для установления равномерной сходимости рядов часто используется простой и эффективный Признак Вейерштрасса.

Ряд равномерно сходится на

Доказательство:

Пусть ряд равномерно сходится.

выполняется условие критерия Коши.

Пусть выполняется условие критерия Коши.

сходится. На всем определена его сумма. Осталось установить равномерную сходимость ряда.

По условию критерия Коши,

: Значит, определение равномерной сходимости проверено.

33) Признак Веерштрасса равномерной сходимости функционального ряда

то ряд сходится абсолютно и равномерно в области

X .

∞

Говорят в этом случае, что числовой ряд åan

n=1

«мажорирует» исходный функциональный ряд, а сам числовой ряд называют мажорантным.

Существует простой признак для проверки равномерной сходимости(принак Вейерштрасса)

Можно рассматривать и при этом сохраняется терминология числовых рядов, связанная с абсолютной и условной сходимостью.

Как и в рядах, абсолютная сходимость сильнее сходимости: из абсолютной сходимости вытекает сходимость.

Теорема (Вейерштрасс):

, ,

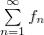— сходится. Тогда равномерно

сходится на . Доказательство: Применим критерий Коши:

Сопоставляя с предыдущим неравенством, которое верно ,

. Тогда, по критерию Коши, ряд равномерно сходится.

34) Степенные ряды. Радиус и область сходимости степенного ряда. Теорема Абеля.

Важным случаем функциональных рядов являются степенные ряды:

Для определения области сходимости степенного ряда используется либо признак Даламбера, либо признак Коши.

Рассмотрим степенной ряд

∞

åcn x n .

n=0

(14)

сходимости ряда.

Формула для радиуса сходимости, получаемая с помощью признака Даламбера, имеет вид

(16)

Область сходимости ряда - так называют множество точек сходимости функционального ряда, т.е. множество значений аргумента х, для которых ряд (бесконечная сумма)

сходится Пример 6.1. Найти область сходимости ряда Область сходимости ряда

что означает, что ряд сходится на всей оси Х.

36) Разложение функций в степенные ряды. Ряд Тейлора. Достаточное условие Разложимости функций в ряд Тейлора.

ряд Тейлора сходится на тогда и только тогда, когда

. теор.: Пусть

и

, тогда на

неравенстве

н а .