
Экзаменационные вопросы по математике / Шпоры по математике
.pdf
1) Определитель. Определение и свойства. Понятие перестановки. Чётность перестановки. Разложение определителя по элементам строки и столбца.
Определитель (детерминант) А n-ого порядка квадратной матрицы А – называется сумма всевозможных произведений из n элементов матрицы, взятых из каждой строки и каждого столбца со знаком, определяющим выражение (-1)ti+tj, где ti – чётность перестановки из индексов строк, а tj – чётность перестановки из индексов столбцов.
Det A = ∑(-1)ti+tjai1j1*ai2j2*ai3j3*…*ainjn.
Перестановкой из n чисел (элементов) называется упорядоченное расположение этих чисел друг за другом.
Инверсия перестановки – изменение порядка следования (большее число идёт за меньшим).
Если общее число инверсий чётное, то перестановка чётная, а если общее число инверсий нечётное – то перестановка нечётная.
Свойства перестановок.
взаимное изменение положение 2х элементов перестановки называется транспозицией.
abcd ->dbca
Утверждение: 1 транспозиция меняет чётность перестановки.
1) Соседние – ai1, ai2, …, aik, aij, …, ain -> ai1, ai2, …, aik, aij, …, ain
2) Несоседние - ai1, ai2, …, aik, aik+1, aik+2 ,…,
aik +p, …, ain - p соседних транспозиций +p-1 = 2p-1
|
|
1 |
2 |
|
3 |
… |
|
… |
n |
n(n+1)(n+2)…*1=n! (произведение последовательных |
|||||||||
натуральных чисел) |
|
|
|
|
|
|
|
|
|
o |
Транспозиция |
|
|
несоседних |
|||||
элементов.
Утверждение: Все n! перестановок из n чисел могут быть расположены последовательно друг за другом так, что каждая последующая перестановка получится из предыдущей путём 1 транспозиции.
Доказательство (метод индукции). 1) n=2 – Утверждение верно.
1 2
2 1
2) Если предположить, что утверждение верно для числа n-1, то из этого следует его справедливость для числа n.
i1,i2,i3,…,in
-зафиксируем 1 элемент и совершим возможные перестановки n-1.
-затем зафиксируем 2 элемент. Осталось n-2
перестановок и т.д.
Из этого следует, что любые 2 перестановки могут быть получены из любой другой конечным числом транспозиций.
n! – всегда чётное число -> если расположить члены друг за другом, то количество чётных перестановок = количеству нечётных.
Вывод: в каждом определителе число отрицательных членов = числу положительных.
Свойства определителей.
Транспонирование не меняет определителя. (Транспонирование – взаимная замена строк и столбцов.)
=
Возьмём любой член определителя (- 1)ti+tjai1j1*ai2j2*ai3j3*…*ainjn.
Из вида любого члена определителя видно, что при транспонировании они не меняются.
det AT = det A
1)Если в определителе поменять местами 2
строки, то знак определителя поменяется на противоположный.
Доказательство: Берём произвольный член определителя. Взаимное расположение -> поменялись первые 2 индекса -> чётность изменилась -> изменился знак.
2) Если в определителе 2 строки (столбца)
одинаковы, то det = 0.
Если 2 одинаковые строки поменять местами, то ничего не меняется, но по св-ву 2 знак меняется. Это происходит, если =0. ( =- , 2 =0, =0)
3)Если в определителе есть 2 пропорциональные строки, то он тоже = 0.
det |
= k det |
после того, как k вынесен, 2 строки равны. По св-ву 3 =0.
4) Если в некоторой строке определителя все
элементы в виде 1 и той же комбинации чисел, а именно k-я строка (αck1 + βdk1 + αck2+ βdk2) = α|ck1+ck2…+ckn|+β|dk1+dk2… +dkn|.
5)Если в любой строке определителя прибавить любую другую строку с противоположным коэффициентом, то определитель не изменится.
6)Если строка в определителе состоит из нулей, то определитель = 0.
7)Если какая-либо строка определителя есть линейная комбинация других строк, то определитель = 0.
1 = (a11,a1n)
2 = (a21,a2n)
n = (an1,ann)
|
1 |
Det A= |
2 |
|
|
|
n |
|
|
Пусть k есть линейная комбинация остальных
k = α1 1 + α2 2 +…+ αk-1
2 +…+ αk-1 k-1 + αk+1
k-1 + αk+1 k+1 +…+ αn
k+1 +…+ αn
n
В соответствии со свойством 7 определитель равен сумме этих определителей, равных нулю. Количество определителей = (n-1)и в каждой из которых имеются одинаковые строки.
Разложение определителя по элементам строки или столбца.
Минором элемента определителя aik называется определитель n-1 порядка, получающийся вычёркиванием строки и столбца, на пересечении которых стоит элемент aik.
Алгебраическим дополнением Аik элемента определителя aik называется Aik = (-1)i+kMik.
Теорема. Определитель равен сумме произведений элементов какой-либо строки на их алгебраические дополнения.
det A = ak1Ak1+ak2Ak2+…+aknAkn =
1)Доказательство: Пусть определитель имеет вид:
=

a11
Определитель 1 порядка, полученный вычёркиванием 1 строки и 1 столбца.
Тем самым, для 1 случая теорема доказана.
2)Пусть определитель имеет вид:
= (-1)j
an1 an2 an3 an4 … anm
Передвинем последовательными шагами столбец этого элемента akj (столбец с номером j) влево до занятия им места 1 столбца. При этом определитель при каждом шаге меняет знак и итоге приобретает множитель (-1)j и приобретает вид:
anj an1 an2 an3 … anm
Далее перемещаем строку с номером k вверх последовательно, пока она не займёт место 1ой строки, т.е. определитель будет иметь вид:
anj an1 an2 an3 … anm
При этом определитель приобретает ещё один множитель (-1)k. В итоге
anj an1 an2 an3 … anm
Мы пришли к 1 случаю, для которого справедливость была доказана.
det A = (-1)j+kakjMkj+0*Ak1+…+0*Ak2 *…*0*Akn
3)Общий случай.
a11 |
a12 |
… |
a1m |
… |
… |
… |
… |
ak1 |
ak2 |
… |
akm |
… |
… |
… |
… |
an1 |
an2 |
… |
anm |
=(-1)k+1ak1Mk1+(-1)k+2ak2Mk2+…+(-1)k+naknMkn
Это правило вычисления определителя называется разложением по I строке (столбцу).
2) Равенство нулю суммы произведений элементов строки (столбца, алгебраическое дополнение другой строки (столбца)).
Сумма произведений элементов какой-либо строки на алгебраическое дополнение другой строки равна нулю, т.е. :
(*) аk1Аj1+ аk2Аj2+…+ аknАjn=0 Доказательство:
Рассмотрим определитель: |
|
|
||||
|
|
|
… |
… |
… … |
|
|
|
|
||||
j-я строка |
|
|
aj1 |
aj2 |
ajn |
= аj1Аj1+ аj2Аj2 |
k-я строка |
|
|
ak1 |
ak2 |
akn |
+…+ аjnАjn (**) |
|
|
|
||||
Ввыражении (*) коэффициент Аjm получились вычёркиванием j-ой строки -> аjmА не зависят от тех чисел, которые могут стоять в j-ой строке.
Вопределителе (**) на место j-ой строки поставим k-ую строчку. Тогда этот определитель равен det А = аk1Аj1+
аk2Аj2+…+ аknАjn
Но это равенство равно нулю, так как определитель имеет две одинаковые строки. Ч.т.д.
3) Ранг матрицы. Вычисление ранга методом окаймляющих миноров.
Пусть имеется прямоугольная матрица nхm .
Минором K-ого порядка матрицы А (k<m,k<n) называется определитель, получающийся из элементов, стоящих на пересечении каких-либо строк и каких-либо столбцов.
Рангом матрицы называется целое, положительное число r=Rang А, такое, что в данной матрице
присутствует хотя бы один минор порядка r≠0, а все миноры следующего порядка (r+1 и далее) =0.
Метод окаймления миноров.
Если в матрице найден отличный от нуля минор k-ого порядка, то все миноры k+1 порядка считать не обязательно, так как имеет место теорема:
Если все окаймляющие данный минор k-ого порядка миноры k+1 порядка равны нулю, то и все вообще миноры k+1 –ого порядка = 0.
Найдём окаймляющие миноры 3-его порядка для M2 : (положим, М2≠0)
а11 |
а12 |
а13 |
а14 |
а21 |
а22 |
а23 |
а24 |
а31 |
а32 |
а33 |
а34 |
а41 |
а42 |
а43 |
а44 |
|
а11 |
а12 |
а13 |
M3(1)= |
а21 |
а22 |
а23 |
|
а31 |
а32 |
а33 |
|
а11 |
а13 |
а14 |
|
|||
M3(2)= |
а21 |
а23 |
а24 |
|
а31 |
а33 |
а34 |
|
а11 |
а12 |
а13 |
|
|||
M3(3)= |
а21 |
а22 |
а23 |
|
а41 |
а42 |
а43 |
|
а11 |
а13 |
а14 |
M3(4)= |
а21 |
а23 |
а24 |
|
а41 |
а43 |
а44 |
4) Теорема о базисном миноре. Понятие линейно независимых строк (столбцов) определителя. Необходимое и достаточное условие равенства 0 определителя.
При нахождении ранга матрицы минор порядка r (ранг матрицы) называется базисным.

Все строки матрицы являются линейными комбинациями строк базисного минора. (к столбцам относится то же самое).
Доказательство:
a11 |
a12 |
… |
a1r |
a1j |
a1r+1 |
… |
a1n |
a21 |
a22 |
… |
a2r |
a2j |
a2r+1 |
… |
a2n |
a31 |
a32 |
… |
a3r |
a3j |
a3r+1 |
… |
a3n |
… |
… |
… |
… |
… |
… |
… |
… |
ar1 |
ar2 |
… |
arr |
arj |
arr+1 |
… |
arn |
|
|
|
|
|
akr+1 |
… |
akn |
ak1 |
ak2 |
… |
akr |
akj |
|||
|
|
|
|
|
amr+1 |
… |
amn |
am1 |
am2 |
… |
amr |
аmj |
|||
|
|
|
|
|
|
|
|
Берём любую строку с номером произвольным k. Ставим её под базисный минор. Вправо от минора ставим произвольный столбец с номером j. Рассмотрим минор Mr+1, окаймляющий базисный снизу. K-ой строкой, справа k-ым столбцом.
Разложим его:
Mr+1=0=c1a1j+ c2a2j+ crarj+ Arakj |:Ar (Ar≠0) Akj=-c1*a1j/Ar- c2*a2j/Ar+…- cr*arj/Ar
Так как akj – координаты вектора строки с номером k, это вернодля любого столбца (коэффициенты ci/Ar одинаковы для любого j) -> сам вектор
строка ak=-c1a1/Ar- c2a1/Ar -crar/Ar Следствие из теоремы о базисном миноре:
Определитель матрицы равен нулю тогда и только тогда, когда ранг матрицы <n (порядок квадратной матрицы)
Доказательство:
а11 а21
аm1 аm2 … аmn
det A = 0 Rang A < n
8) Необходимость: дано: det A = 0,
доказать: Rang A<n
Так как det A = 0, то по карйней мере одна из строк есть линейная комбинация строк. Это значит, что число линейно независимых строк < n. Число линейно независимых строк и есть Rang A -> r<n
9) Достаточность: дано: Rang A<n,
доказать: det A = 0
Так как Rang A<n, а ранг – число линейно независимых строк, то в А число линейно независимых строк <n. Значит, по крайней мере одна из строк есть линейная комбинация остальных, а это значит, что det A = 0 (по св-вам определителя).
Ранг матрицы равен числу линейно независимых строк (столбцов), так как если методом Гаусса с помощью элементарных преобразований привести матрицу к виду трапеции, то оставшиеся строки являются линейно независимыми.
а11 |
а12 |
… |
а1n |
а21 |
а22 |
… |
а2n |
аm1 |
аm2 |
… |
аmn |
Рассмотрим строки как векторы (координаты aij (j=1,2,3…n))
1=(а11, а12, а13,…,а1n);
2=(а21, а22, а23,…,а2n);
m=(аm1, аm2, аm3,…,аmn);
Строки называются линейно независимыми, если они линейно независимы в смысле векторов, т.е.
единственная линейная комбинация векторов, равная 0, это та, все коэффициенты нули.
Линейная комбинация – с1 1 + с2
1 + с2 2 + … + сm
2 + … + сm m равна
m равна
нулю тогда и только тогда, когда все числовые коэффициенты с1 = с2 = сn = 0. Тогда векторы линейно независимы.
Если вектор – линейная комбинация остальных, то система линейно зависима: ak= с1 1 + с2
1 + с2 2 + … + сk-1
2 + … + сk-1
 k-1 + сk+1
k-1 + сk+1 k+1 + сn
k+1 + сn n
n
5) Системы линейных алгебраических уравнений. Правило Крамера.
х1, х2, …, хn – неизвестные
aik – постоянные коэффициенты
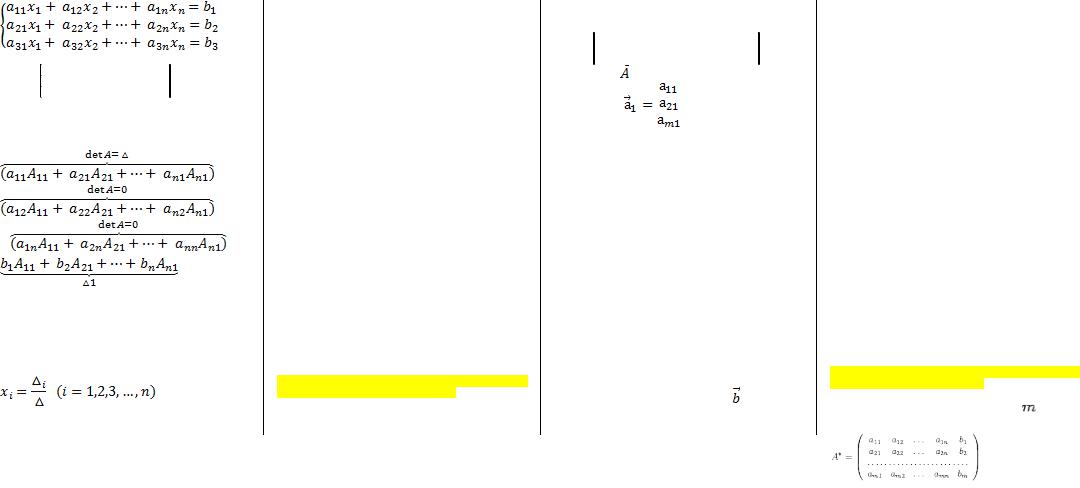
Матрица системы: |
|
|
||
|
а11 |
а12 |
… |
а1n |
|
а21 |
а22 |
… |
а2n |
|
аm1 |
аm2 |
… |
аmn |
10) Кмножаем каждую строку системы на алгебраическое дополнение 1-ого элемента строки.
11)Сложим уравнения.
*x1 +
*x2 + …
+ |
*xn = |
12) Поступим так же со вторым столбцом. (каждый элемент строки умножаем на А второго элемента
строки). Слева получим х2 , справа -
2 Если определитель системы ≠0, то система имеет, и
притом единственное, решение, даваемое формулами крамера:
– определитель системы, составленный из коэффициентов при неизвестных.
i – определитель, получаемый из определителя системы заменой столбца коэффициентов при неизвестном определяемом столбце свободных членов. Если определитель системы = 0:
Если хотя бы один i ≠ 0, то система несовместна (ᴓ) (решений нет)
Если все i = 0, то решение существует и их бесконечно много. Система несовместна и называется неопределённой.
В случае неопределённой системы не все числа х1, х2, … , хn можно брать произвольными, так как даже если одно уравнение осталось в системе, а все остальные – следствие из него, то это уравнение связывает между собой переменные, а это и значит, что все их брать произвольными нельзя.
6) Необходимое и достаточное условие совместимости системы. Теорема Кронекера – Капелле.
Система совместна тогда и только тогда, когда Rang А, составленный из коэффициентов при неизвестных,
равен Rang Yрасширенной матрицы, т.е. матрицы, которая получена из матрицы A присоединением к ней столбца свободных членов.
а11 |
а12 |
… |
а1n |
b1 |
а21 |
а22 |
… |
а2n |
b2 |
аm1 |
аm2 |
… |
аmn |
b3 |
Rang A = Rang Вектор столбец
(*) a1x1 + a2x2 +…+ anxn =b
1) Необходимость: Дано: совместная система, доказать: Rang A = Rang 
Доказательство: Так как система совместна, то есть, имеет решение, то существует такой набор чисел x1=c1 , x2=c2 , xn=cn , при подставлении которых в систему (*) получится верное равенство. Следовательно, b есть линейная комбинация остальных столбцов.
 1x1 +
1x1 +  2x2 +…+
2x2 +…+  nxn =
nxn =
->  линейная комбинация столбцов
линейная комбинация столбцов  . Если в матрице
. Если в матрице
 один столбец является линейной комбинацией остальных, то при добавлении к матрице А этого столбца, её Rang не меняется, т.е. Rang A = Rang
один столбец является линейной комбинацией остальных, то при добавлении к матрице А этого столбца, её Rang не меняется, т.е. Rang A = Rang 
2) Достаточность:
Дано: Rang A = Rang  Доказать: система (*) совместна.
Доказать: система (*) совместна.
Доказательство: Матрицы A и  отличаются только
отличаются только  и
и
т.к. их ранги равны, то дабавление к А не меняет её
ранга. Значит, этот столбец – линейная комбинация остальных столбцов. Т.е. существует такие числа c1, c2,
c3,…,cn, что  1c1+
1c1+  2c2+…+
2c2+…+ ncn=
ncn= . Но это и есть
. Но это и есть
система (*)
-> (*) удовлетворилась при x1=c1, x2=c2, xn=cn ч.т.д. Т.е. с1,с2,сn – решения системы.
7) Метод Гаусса решения систем линейных алгебраических систем уравнений.
Метод Гаусса. Пусть дана система |
линейных |
уравнений с  неизвестными
неизвестными  . Выпишем
. Выпишем

расширенную матрицу системы/ |
Цель алгоритма -- с |
|
помощью |
применения |
последовательности |
элементарных операций к матрице  добиться, чтобы каждая строка, кроме, быть может, первой, начиналась с нулей, и число нулей до первого ненулевого элемента в каждой следующей строке было больше, чем в предыдущей. Находим первый ненулевой
добиться, чтобы каждая строка, кроме, быть может, первой, начиналась с нулей, и число нулей до первого ненулевого элемента в каждой следующей строке было больше, чем в предыдущей. Находим первый ненулевой
столбец в матрице  . Пусть это будет столбец с
. Пусть это будет столбец с
номером  . Находим в нем ненулевой элемент и строку с этим элементом меняем местами с первой строкой. Чтобы не нагромождать дополнительных обозначений,
. Находим в нем ненулевой элемент и строку с этим элементом меняем местами с первой строкой. Чтобы не нагромождать дополнительных обозначений,
будем считать, что такая смена строк в матрице 
уже произведена, то есть |
. Тогда ко второй |
строке прибавим первую, |
умноженную на число |
,к третьей строке прибавим первую,
умноженную на число |
, и т.д. В результате |
получим матрицу |
|
Если в матрице |
встретилась строка с номером |
, |
|
в которой все элементы |
равны нулю, а |
, |
|
то выполнение |
алгоритма останавливаем и делаем |
||
вывод, что система |
несовместна. Действительно, |
||
восстанавливая систему уравнений по расширенной матрице, получим, что  -ое уравнение будет иметь вид
-ое уравнение будет иметь вид
Этому уравнению не удовлетворяет ни один набор
чисел |
Матрицу |
можно |
записать в виде |
|
|
|
|
где |
По отношению к матрице выполняем описанный шаг алгоритма. Получаем матрицу
 гд
гд
е  ,
,  . Эту матрицу снова можно записать в виде
. Эту матрицу снова можно записать в виде
и к матрице снова применим описанный выше шаг алгоритма.
Процесс останавливается, если после выполнения очередного шага новая уменьшенная матрица состоит из одних нулей или если исчерпаны все строки. Заметим, что заключение о несовместности системы могло остановить процесс и ранее. Если бы мы не уменьшали матрицу, то в итоге пришли бы к матрице вида
Далее выполняется так называемый обратный ход
метода Гаусса. По матрице  составляем систему уравнений. В левой части оставляем неизвестные с номерами, соответствующими первым ненулевым
составляем систему уравнений. В левой части оставляем неизвестные с номерами, соответствующими первым ненулевым
элементам в каждой строке, то есть  .
.
Заметим, что . Остальные неизвестные переносим в правую часть. Считая неизвестные в правой части некоторыми фиксированными величинами, несложно выразить через них неизвестные левой части. Теперь, придавая неизвестным в правой части произвольные значения и вычисляя значения переменных левой части, мы будем находить различные
решения исходной системы  . Чтобы записать общее решение, нужно неизвестные в правой части обозначить в каком-либо порядке буквами
. Чтобы записать общее решение, нужно неизвестные в правой части обозначить в каком-либо порядке буквами
,включая и те неизвестные,
которые явно не выписаны в правой части из-за нулевых коэффициентов, и тогда столбец неизвестных можно записать в виде столбца, где каждый элемент будет линейной комбинацией произвольных величин
(в частности, просто произвольной
величиной  ). Эта запись и будет общим решением системы. Если система была однородной, то получим общее решение однородной системы. Коэффициенты
). Эта запись и будет общим решением системы. Если система была однородной, то получим общее решение однородной системы. Коэффициенты
при |
, взятые в каждом элементе столбца общего |
||||||
решения, |
составят |
первое |
решение |
из |
|||
фундаментальной |
системы |
решений, |
коэффициенты |
||||
при |
-- |
второе |
решение |
и т.д. Фундаментальную |
|||
систему решений однородной системы можно получить и другим способом. Для этого одному переменному, перенесенному в правую часть, нужно присвоить значение 1, а остальным -- нули. Вычислив значения переменных в левой части, получим одно решение из фундаментальной системы. Присвоив другому переменному в правой части значение 1, а остальным -- нули, получим второе решение из фундаментальной системы и т.д. Замечание 15.4 У читателя может возникнуть вопрос: "Зачем рассматривать случай, когда
некоторые столбцы матрицы  нулевые? Ведь в этом случае соответствующие им переменные в системе уравнений в явном виде отсутствуют." Но дело том, что в некоторых задачах, например, при нахождении собственных чисел матрицы, такие системы возникают, и игнорировать отсутствующие переменные нельзя, так как при этом происходит потеря важных для задачи.
нулевые? Ведь в этом случае соответствующие им переменные в системе уравнений в явном виде отсутствуют." Но дело том, что в некоторых задачах, например, при нахождении собственных чисел матрицы, такие системы возникают, и игнорировать отсутствующие переменные нельзя, так как при этом происходит потеря важных для задачи.

8) Однородная система алгебраических уравнений. Необходимое и достаточное условия существования ненулевых решений. Понятие фундаментальной системы решений однородной системы уравнений (ФСР). Еѐ общее решение.
Особенность однородной системы алгебраических уравнений в том, что она всегда совместна.
Тривиальное решение: x1=x2=…=xn=0.
При исследовании однородных систем необходимо выяснить, когда, кроме тривиальных решений, есть нетривиальные.
Запишем систему в сокращенной (матричной) форме.
 =
=
A=0
Предположим, что нетривиальное решение существует: r=RangA<n. (n-r) – линейная зависимость строк, столбцов.
Выделяем минор порядка r. Оставшиеся уравнения (n-r) – линейная комбинация базисных r строк, т.е. эти уравнения можно вычислить как следствие базисных. После этого осталось r линейно независимых строк (уравнений).
минор не равен 0.
Перенесем неизвестные, не входящие в базисный минор направо. Они называются свободными. А те, которые в базисном, x1, x2, …, xr – главные неизвестные.
Если переменным справа придать любые значения, то по правилу Крамера x1, x2, …, xr будут иметь одно однородное определенное значение. Таким образом, можно получить всевозможные решения системы.
 =
=
Если r<n, то система имеет бесконечно много решений, которые можно записать в виде векторных столбцов. А к векторам применима линейная независимость. Согласно линейной независимости векторов, решения будут
линейно независимы, когда существует такая их линейная комбинация C1X1+C2X2+…=0, в которой коэффициент C=0.
9) Общее решение неоднородной системы линейных алгебраических уравнений.
(*)
Система неоднородна, если хотя бы одно из чиел bn не равно 0.
Запишем систему (*) в векторном виде:

= |
= |
A= |
A =
=
Утверждение:
Два различных решения неоднородной системы могут отличаться только на решение однородной системы, т.е.: пусть Y1 – решение неоднородной системы;
пусть Y2 – решение неоднородной системы;
тогда Y1-Y2=решение однородной системы. Доказательство:
Т.к. AY1=B, AY2=B Вычитаем: AY1-AY2=0
A(Y1-Y2)=0, т.е. Y1-Y2= решение однородной системы.
Т.е. если мы имеем одно решение неоднородной системы Y, то любое другое решение отличается на решение однородной системы.
Одно какое-то решение Y – частное решение неоднородной системы.
Все решения неоднородной системы получим прибавив к Y общее решение соответствующей однородной системы.
Если Y частное имеет вид |
=Y0, то: |
, где |
, |
, …, |
– образованыиз решений |
однородных систем.
Найдем частное решение:
=Y0+C1X1+C2X2+…Cn-rXn-r=
+C1 |
+C2 |
+Cn-r |
Проще всего получить частное решение неоднородной системы, положив все свободные члены справа равными 0, т.е.:
Отсюда по правилу Крамера получим единственные решение для y1, y2, …, yr, т.е. частное решение, которое имеет вид:
Таким образом, общее решение неоднородной системы имеет вид:
10) Первообразная функции. Свойства первообразной. Теорема об общем виде первообразной.
Если на некотором промежутке задана функция f(x), а функция F(x) на этом же промежутке дифференцируема и в каждой точке F’(x)=f(x), то функция F(x) называется первообразной для функции f(x) на этом промежутке.
Пример: Предположим, имеется функция:

f(x)= |
, x |
|
. Найти F(x). F(x)=arcsinx. |
|
Пусть |
|
во всех точках некоторого промежутка имеет |
f(x)= |
F(x)=arcsinx. |
|
|
18) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
производную |
|
|
. |
|
Совокупность всех первообразных функции f(x) на данном |
19) |
|
|
|
||||||
Свойства первообразных: |
|
|
|
|
Докажем то, что |
|
на этом промежутке. Т.к. |
промежутке называется неопределенным интегралом |
этой |
|
|
|
|||||||||||
|
13) Если F(x) есть первообразная для f(x) |
|
функции. |
|
|
|
(A=const) |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
имеет |
производную, |
то |
x |
|
|
|
|
|
|
|
|
|
||||||||||
|
на |
промежутке, |
тогда F(x)+C |
|
тоже |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
первообразная для f(x), где C – произвольная |
|
|
|
|
. |
|
Таблица интегралов: |
|
|
|
|
|
|
|
|
|||||||
|
постоянная. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Доказательство: |
|
|
|
|
|
|
|
|
|
|
, |
. |
f(x) |
F(x) |
f(x) |
F(x) |
|
|
|
|
|
|
|
(F(x)+C)’=F(x)’+C’=F’(x)=f(x). |
|
|
|
|
|
|
|
|
0 |
const |
sin x |
-cos x |
|
|
|
|
|
|
|||||
|
|
|
|
Т.к. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
14) Если F(x) – первообразная для f(x) на |
|
|
|
|
|
C |
Cx+C1 |
cos x |
sin x |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
x |
|
|
tg x |
|
|
|
|
|
|
|||||||
|
промежутке, то для функции f(kx+b) (k,b |
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
const) |
первообразной |
будет |
функция |
Теорема: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
(1/k)F(kx+b). |
|
|
|
|
|
|
|
|
xn |
|
|
-ctg x |
|
|
|
|
|
|
||||
Доказательство: |
|
|
|
|
|
|
Докажем, что первообразная отличается только на |
const. |
|
|
|
|
|
|
|
|
|||||||
((1/k)F(kx+b))’=(1/k)F’(kx+b)=(1/k)f(kx+b) |
|
|
F1(x)-F2(x)=C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(kx+b)’=(1/k)f(kx+b)k=f(kx+b). |
|
|
|
|
F’1(x)=f(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Свойство линейной замены переменных: |
|
|
|
F’2(x)=f(x) |
|
|
|
|
|
ln x |
|
arcsin x |
|
|
|
|
|
|
|||||
|
|
|
Рассмотрим |
функцию |
|
. |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пусть f(x)= |
|
, k=3 |
|
|
|
|
Вычислим производную этой функции: |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ex |
ea |
|
arctg x |
|
|
|
|
|
|
Найдем первообразную для функции |
|
, тогда F(x)= |
, |
по лемме следует, что |
|
, F1(x)-F2(x)=C, ч.т.д. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
тогда F=1/3 |
|
|
|
|
|
|
|
+C=f(x) – общий вид. |
|
|
ax |
|
|
ln(x+ |
) |
|
|
|
|
|
|||
f(x)= |
, k=-1/x, F= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15) |
|
Основное свойство первообразной |
|
|
|
|
|
|
|
|
|
½ ln |
|
|
|
|
|
|
||||
Две различные первообразные одной и той же функции могут |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
отличаться только на постоянное значение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Лемма Ла-Гранжа: |
|
|
|
|
|
|
11) Неопределенный интеграл. Основные свойства. Таблица. |
Свойства: |
|
|
|
|
|
|
|
|
|||||||
Если |
производная |
некоторой функции |
тождественно равна |
Если |
на некотором |
промежутке задана функция |
f(x), а |
|
|
|
|
|
|
|
|
||||||||
|
16)d |
|
|
|
12) Интегрирование по частям и заменой переменных. |
|
|||||||||||||||||
нулю на некотором промежутке, то функция тождественно |
функция F(x) на этом же промежутке дифференцируема и в |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
равна постоянной на этом промежутке. |
|
|
|
каждой точке F’(x)=f(x), то функция F(x) называется |
|
17) |
|
|
|
Пусть |
функция |
определена |
и |
||||||||||
Доказательство: |
|
|
|
|
|
|
первообразной для функции f(x) на этом промежутке. |
|
|
|
|
|
дифференцируема на некотором множестве |
и пусть |
|||||||||
|
|
|
|
|
|
|
|
Пример: |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

– множество всех значений этой функции. Пусть
далее для |
функции |
существует |
множество |
||
первообразная |
|
функция |
|
. |
|
|
|
|
. Тогда всюду на множестве |
||
для |
функции |
|
существует |
||
первообразная |
функция, |
равная |
|
, т.е. |
|
|
|
|
|
. |
Для |
доказательства |
достаточно воспользоваться |
правилом |
|||
дифференцирования |
сложной |
|
функции: |
||
|
|
|
|
и учесть, что |
|
по определению первообразной |
|
. |
|||
Предположим теперь, что нам требуется вычислить
интеграл |
. В качестве новой переменной |
|
выберем |
что |
|
причем функция |
g(t) легко интегрируется, т.е.: |
|
|
просто |
вычисляется. |
Интегрирование путем замены переменной
Замена:
Интегрирование по частям
Пусть каждая из функций |
и |
дифференцируема на множестве  и, кроме того, на этом множестве существует первообразная для функции
и, кроме того, на этом множестве существует первообразная для функции  . Тогда на множестве
. Тогда на множестве 
существует первообразная и для функции |
, |
|
причем |
справедлива |
формула: |
Замечание: Определение дифференциала и свойство инвариантности его формы позволяет записать
формулу в виде  Для доказательства утверждения запишем формулу для
Для доказательства утверждения запишем формулу для
производной произведения 2-х функций |
|
и |
: |
||
|
|
|
. |
Умножим |
|
равенство на |
и возьмем интеграл от обеих частей |
||||
равенства. Так как по условию для всех |
из множества |
||||
существует |
|
|
|
и |
|
|
, |
то |
для |
всех |
|
множества |
существует интеграл |
|
|
|
, |
причем |
справедлива |
|
формула: |
||
|
. Эта |
формула |
сводит |
||
вопрос о вычислении интеграла |
|
к вычислению |
|||
. |
. |
|
|
|
|
13) Интегрирование рациональных функций. Теорема о разложении дробно-рациональной функции на элементарные дроби. Интегрирование элементарных функций.

P (x ) |
- алгебраическая дробь, отношение 2х |
Q (x ) |
многочленов.
Из неправильной можно выделить правильную путем деления (то, что получилось + остаток / то, на что делили)
P (x )
Интегрирование правильной дроби - Q (x )
Теорема. Если многочлен, стоящий в знаменателе, имеет
корень x=a, то есть |
представленный в |
виде |
Q( x)=(x−a)α φ( x) |
(φ(a)!=0) (α |
- |
кратность корня) (α >=1)
х=а называется корнем многочлена Q(x), если Q(a)=0.
Теорема Безу. Остаток R от деления многочлена Q(x) на двучлен (x-a) равен R=Q(a).
Д-во: Делим |
Q( x) |
=φ( x)+ |
Rчисло |
| *(x-a) |
|
(x −a) |
(x−a) |
||||
|
|
|
φ (x) – многочлен, степень на 1 меньше Q(x)
Q( x)=φ(x ) ( x−a )+ R
Положим х=а, следовательно, Q(a)=R
Пример. Не производя деления найдем остаток от деления многочлена Q( x)=2x4−x3+ 3x2−5x+ 3 на
(х-1). Q(1)=2-1+3-5+3=2
Следствие. Если многочлен Q(x) имеет корень а, то есть Q(a)=0, то его можно представить в виде Q( x)=(x−a)m φ( x) , где φ (а)!=0
Разделим Q(x) на (х-а), получим φ(х)+R, по теореме Безу R=Q(a)=0, то есть Q(x)=(x-a)φ(x)
Q(x)=(x-a)(x-b)(x-c)...
P (x )
Теорема. Если Q (x ) - правильная алгебраическая дробь, знаменатель которой Q(x) имеет корень а кратности α>=1, то
|
P (x ) |
= |
|
A |
|
|
+ |
|
ψ ( x) |
|
|
, где |
|||||||||
|
|
|
|
(x−a)α |
( x−a )α−k φ( x) |
||||||||||||||||
|
Q (x ) |
|
|
|
|
|
|
|
|||||||||||||
1<=k<=α и воторое слагаемое есть правльная алгебраическая |
|||||||||||||||||||||
дробь. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Док-во. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
P (x ) |
= |
P ( x) |
− |
|
|
|
|
A |
+ |
|
A |
= |
|
|||||||
|
|
|
Q( x) |
|
( x−a )α |
(x −a)α |
(x− |
||||||||||||||
|
Q (x ) |
|
|
|
|
|
|
|
|
||||||||||||
Q( x)=(x−a)α φ( x) (φ(a)!=0) |
|
|
|
|
|||||||||||||||||
|
P (x ) |
− |
|
A |
|
|
|
|
= |
|
|
|
|
|
|
|
|
||||
|
|
|
|
(x−a)α |
|
|
|
|
|
|
|
|
|
|
|||||||
|
Q (x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
P( x) |
|
− |
|
|
A |
|
(домножаем на |
||||||||||||
|
|
|
|
|
α |
|
|
|
|
|
α |
||||||||||
|
(x −a) φ( x) |
|
|
|
( x−a ) |
|
|
|
|
|
|
|
|||||||||
|
|
P( x)−A φ(x ) |
|
|
|
|
|
|
|
|
|||||||||||
= |
|
= |
|
|
|
|
|
|
|
||||||||||||
( x−a)α φ (x) |
|
|
|
|
|
|
|
||||||||||||||
(x−a) ψ (x) ψ (x )
(x −a)α φ( x) = (x −a)α φ( x) ч.т.д.
(P (x )− A φ( x)=Φ ( х))
А возьмем таким образом, чтобы Р(а)-А*φ(а)=0, т. е.
AP (a)
=ψ (a ) , следовательно, многочлен Φ имеет корень
а, |
значит, |
по |
теореме |
Безу |
Φ (x )=( x−a )k ψ (x) , где ψ(а)!=0 |
|
|||
|
P (x ) |
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|||||||
|
|
|
|
|
- правильная дробь, |
|
(x −a)α |
- правильная, |
|||||||||||||||
|
Q (x ) |
||||||||||||||||||||||
следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
P (x ) |
= |
|
|
|
A |
+ |
|
|
|
ψ ( x) |
|
|
- |
|||||||||
|
|
|
(x−a)α |
|
( x−a )α φ(x ) |
||||||||||||||||||
|
Q (x ) |
|
|
|
|
|
|||||||||||||||||
правильная! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
P (x ) |
= |
|
|
|
A |
|
+ |
|
ψ (x ) |
= |
|
|
|
|
|
|
||||||
|
|
|
|
(x−a)α |
|
|
|
|
|
|
|
|
|||||||||||
|
Q (x ) |
|
|
|
Q1 (x ) |
|
|
|
|
|
|
||||||||||||
|
|
A |
|
+ |
B |
|
|
|
+ |
|
|
X ( x) |
|
|
|||||||||
|
(x |
|
|
|
α |
|
(x−b) |
β |
(x−b) |
β−m |
φ1 (x ) |
||||||||||||
|
−a) |
|
|
|
|
|
|||||||||||||||||
Если |
многочлен Q1 (x ) |
|
имеет корень b, |
то |
|||||||||||||||||||
Q1 (x )=(x−b)β φ1 ( x)
В частности, если b=a, то есть Q1(x) имеет корень а, то
|
P (x ) |
= |
P ( x) |
− |
|
A |
|
+ |
A |
= |
|
|||
|
Q (x ) |
Q( x) |
( x−a )α |
(x −a)α |
(x− |
|||||||||
|
|
|
|
|
||||||||||
+ |
|
A1 |
+ |
|
A2 |
|
+ ... + |
|
|
|||||
|
(x −b)β |
(x −b)β−1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||
Ζ(дзета )+ ...
x−b
Если а — комплексный корень множества Q(x), то корнем будет и комплексное сопряженное число, то есть a=α+iβ,
Например. |
|
|
D<0 |
|
|
ax2 + bx+ c . |
Его |
корень |
x1,2=−b±√ b2−4ac
2a
Если D=b2 −4ac< 0 , то 2 комплексных корня
x1,2=−b±i √ D
2a
Q( x)=(x−a) (x −̄a) φ(x ) = =
(x2−(a+ ā) x+ a ā) φ( x) = (x2−2αx+ α2+ β2) φ( x)
Q( x)=(x2+ px + q)γ φ(x )
P (x ) |
M x+ N |
|
ψ ( x) |
|
|
= |
|
+ |
|
Q (x ) |
(x2+ px+ q)γ |
(x2 + px+ q)γ−k φ |
||
Доказательство аналогичное.
Вывод. Всякая правильная алгебраическая дробь может быть разложена на сумму элементарных дробей:
|
P (x ) |
= |
|
|
A1 |
|
+ |
|
A2 |
+ ...+ |
Aα |
||
|
Q (x ) |
(x−a)α |
( x−a )α−1 |
x−a |
|||||||||
|
|
|
|
||||||||||
+ |
|
B1 |
|
+ |
|
|
B2 |
|
+ ... + |
|
|
||
|
(x −b)β |
|
(x −b)β−1 |
|
|
||||||||
|
|
|
|
|
|
|
|||||||
