4) Теорема о базисном миноре. Понятие линейно независимых строк (столбцов) определителя. Необходимое и достаточное условие равенства 0 определителя.

При нахождении ранга матрицы минор порядка r (ранг матрицы) называется базисным.

Все строки матрицы являются линейными комбинациями строк базисного минора. (к столбцам относится то же самое).

Доказательство:

a11	a12	…	a1r	a1j	a1r+1	…	a1n
a21	a22	…	a2r	a2j	a2r+1	…	a2n
a31	a32	…	a3r	a3j	a3r+1	…	a3n
…	…	…	…	…	…	…	…
ar1	ar2	…	arr	arj	arr+1	…	arn
ak1	ak2	…	akr	akj	akr+1	…	akn
am1	am2	…	amr	аmj	amr+1	…	amn

Берём любую строку с номером произвольным k. Ставим её под базисный минор. Вправо от минора ставим произвольный столбец с номером j. Рассмотрим минор Mr+1, окаймляющий базисный снизу. K-ой строкой, справа k-ым столбцом.

Разложим его:

Mr+1=0=c1a1j+ c2a2j+ crarj+ Arakj |:Ar (Ar≠0)

Akj=-c1*a1j/Ar- c2*a2j/Ar+…- cr*arj/Ar

Так как akj – координаты вектора строки с номером k, это вернодля любого столбца (коэффициенты ci/Ar одинаковы для любого j) -> сам вектор

строка ak=-c1a1/Ar- c2a1/Ar -crar/Ar

Следствие из теоремы о базисном миноре:

Определитель матрицы равен нулю тогда и только тогда, когда ранг матрицы <n (порядок квадратной матрицы)

Доказательство:

а11	а12	…	а1n
а21	а22	…	а2n
аm1	аm2	…	аmn

det A = 0

Rang A < n

8. Необходимость: дано: det A = 0, доказать: Rang A<n

Так как det A = 0, то по карйней мере одна из строк есть линейная комбинация строк. Это значит, что число линейно независимых строк < n. Число линейно независимых строк и есть Rang A -> r<n

9. Достаточность: дано: Rang A<n, доказать: det A = 0

Так как Rang A<n, а ранг – число линейно независимых строк, то в А число линейно независимых строк <n. Значит, по крайней мере одна из строк есть линейная комбинация остальных, а это значит, что det A = 0 (по св-вам определителя).

Ранг матрицы равен числу линейно независимых строк (столбцов), так как если методом Гаусса с помощью элементарных преобразований привести матрицу к виду трапеции, то оставшиеся строки являются линейно независимыми.

а11	а12	…	а1n
а21	а22	…	а2n
аm1	аm2	…	аmn

Рассмотрим строки как векторы (координаты aij (j=1,2,3…n))

1=(а11, а12, а13,…,а1n);

2=(а21, а22, а23,…,а2n);

m=(аm1, аm2, аm3,…,аmn);

Строки называются линейно независимыми, если они линейно независимы в смысле векторов, т.е. единственная линейная комбинация векторов, равная 0, это та, все коэффициенты нули.

Линейная комбинация – с11 + с22 + … + сmm равна нулю тогда и только тогда, когда все числовые коэффициенты с1 = с2 = сn = 0. Тогда векторы линейно независимы.

Если вектор – линейная комбинация остальных, то система линейно зависима: ak= с11 + с22 + … + сk-1k-1 + сk+1k+1 + сnn

5) Системы линейных алгебраических уравнений. Правило Крамера.

х1, х2, …, хn – неизвестные

aik – постоянные коэффициенты

Матрица системы:

а11	а12	…	а1n
а21	а22	…	а2n
аm1	аm2	…	аmn

10. Кмножаем каждую строку системы на алгебраическое дополнение 1-ого элемента строки.

11. Сложим уравнения.

*x1 + *x2 + … + *xn =

12. Поступим так же со вторым столбцом. (каждый элемент строки умножаем на А второго элемента строки). Слева получим △х2 , справа - △2

Если определитель системы △≠0, то система имеет, и притом единственное, решение, даваемое формулами крамера:

△ – определитель системы, составленный из коэффициентов при неизвестных.

△i – определитель, получаемый из определителя системы △ заменой столбца коэффициентов при неизвестном определяемом столбце свободных членов.

Если определитель системы △ = 0:

Если хотя бы один △i ≠ 0, то система несовместна (ᴓ) (решений нет)

Если все △i = 0, то решение существует и их бесконечно много. Система несовместна и называется неопределённой.

В случае неопределённой системы не все числа х1, х2, … , хn можно брать произвольными, так как даже если одно уравнение осталось в системе, а все остальные – следствие из него, то это уравнение связывает между собой переменные, а это и значит, что все их брать произвольными нельзя.

6) Необходимое и достаточное условие совместимости системы. Теорема Кронекера – Капелле.

Система совместна тогда и только тогда, когда Rang А, составленный из коэффициентов при неизвестных, равен Rang Yрасширенной матрицы, т.е. матрицы, которая получена из матрицы A присоединением к ней столбца свободных членов.

а11	а12	…	а1n	b1
а21	а22	…	а2n	b2
аm1	аm2	…	аmn	b3

Rang A = Rang

Вектор столбец

(*) a1x1 + a2x2 +…+ anxn =b

1) Необходимость: Дано: совместная система, доказать: Rang A = Rang

Доказательство: Так как система совместна, то есть, имеет решение, то существует такой набор чисел x1=c1 , x2=c2 , xn=cn , при подставлении которых в систему (*) получится верное равенство. Следовательно, b есть линейная комбинация остальных столбцов.

1x1 + 2x2 +…+ nxn =

-> линейная комбинация столбцов . Если в матрице один столбец является линейной комбинацией остальных, то при добавлении к матрице А этого столбца, её Rang не меняется, т.е. Rang A = Rang

2) Достаточность:

Дано: Rang A = Rang

Доказать: система (*) совместна.

Доказательство: Матрицы A и отличаются только и т.к. их ранги равны, то дабавление к А не меняет её ранга. Значит, этот столбец – линейная комбинация остальных столбцов. Т.е. существует такие числа c1, c2, c3,…,cn, что 1c1+ 2c2+…+ncn= . Но это и есть система (*)

-> (*) удовлетворилась при x1=c1, x2=c2, xn=cn ч.т.д.

Т.е. с1,с2,сn – решения системы.

7) Метод Гаусса решения систем линейных алгебраических систем уравнений.

Метод Гаусса. Пусть дана система линейных уравнений с неизвестными . Выпишем расширенную матрицу системы/ Цель алгоритма -- с помощью применения последовательности элементарных операций к матрице добиться, чтобы каждая строка, кроме, быть может, первой, начиналась с нулей, и число нулей до первого ненулевого элемента в каждой следующей строке было больше, чем в предыдущей. Находим первый ненулевой столбец в матрице . Пусть это будет столбец с номером . Находим в нем ненулевой элемент и строку с этим элементом меняем местами с первой строкой. Чтобы не нагромождать дополнительных обозначений, будем считать, что такая смена строк в матрице уже произведена, то есть . Тогда ко второй строке прибавим первую, умноженную на число , к третьей строке прибавим первую, умноженную на число , и т.д. В результате получим матрицу

Если в матрице встретилась строка с номером , в которой все элементы равны нулю, а , то выполнение алгоритма останавливаем и делаем вывод, что система несовместна. Действительно, восстанавливая систему уравнений по расширенной матрице, получим, что -ое уравнение будет иметь вид

Этому уравнению не удовлетворяет ни один набор чисел Матрицу можно записать в виде

где

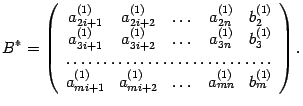
По отношению к матрице выполняем описанный шаг алгоритма. Получаем матрицу

где , . Эту матрицу снова можно записать в виде

и к матрице снова применим описанный выше шаг алгоритма.

Процесс останавливается, если после выполнения очередного шага новая уменьшенная матрица состоит из одних нулей или если исчерпаны все строки. Заметим, что заключение о несовместности системы могло остановить процесс и ранее. Если бы мы не уменьшали матрицу, то в итоге пришли бы к матрице вида

Далее выполняется так называемый обратный ход метода Гаусса. По матрице составляем систему уравнений. В левой части оставляем неизвестные с номерами, соответствующими первым ненулевым элементам в каждой строке, то есть . Заметим, что . Остальные неизвестные переносим в правую часть. Считая неизвестные в правой части некоторыми фиксированными величинами, несложно выразить через них неизвестные левой части. Теперь, придавая неизвестным в правой части произвольные значения и вычисляя значения переменных левой части, мы будем находить различные решения исходной системы . Чтобы записать общее решение, нужно неизвестные в правой части обозначить в каком-либо порядке буквами , включая и те неизвестные, которые явно не выписаны в правой части из-за нулевых коэффициентов, и тогда столбец неизвестных можно записать в виде столбца, где каждый элемент будет линейной комбинацией произвольных величин (в частности, просто произвольной величиной ). Эта запись и будет общим решением системы. Если система была однородной, то получим общее решение однородной системы. Коэффициенты при , взятые в каждом элементе столбца общего решения, составят первое решение из фундаментальной системы решений, коэффициенты при  -- второе решение и т.д. Фундаментальную систему решений однородной системы можно получить и другим способом. Для этого одному переменному, перенесенному в правую часть, нужно присвоить значение 1, а остальным -- нули. Вычислив значения переменных в левой части, получим одно решение из фундаментальной системы. Присвоив другому переменному в правой части значение 1, а остальным -- нули, получим второе решение из фундаментальной системы и т.д. Замечание 15.4   У читателя может возникнуть вопрос: "Зачем рассматривать случай, когда некоторые столбцы матрицы нулевые? Ведь в этом случае соответствующие им переменные в системе уравнений в явном виде отсутствуют." Но дело том, что в некоторых задачах, например, при нахождении собственных чисел матрицы, такие системы возникают, и игнорировать отсутствующие переменные нельзя, так как при этом происходит потеря важных для задачи.

8) Однородная система алгебраических уравнений. Необходимое и достаточное условия существования ненулевых решений. Понятие фундаментальной системы решений однородной системы уравнений (ФСР). Еѐ общее решение.

Особенность однородной системы алгебраических уравнений в том, что она всегда совместна.

Тривиальное решение: x1=x2=…=xn=0.

При исследовании однородных систем необходимо выяснить, когда, кроме тривиальных решений, есть нетривиальные.

Запишем систему в сокращенной (матричной) форме.

=

A=0

Предположим, что нетривиальное решение существует: r=RangA<n. (n-r) – линейная зависимость строк, столбцов.

Выделяем минор порядка r. Оставшиеся уравнения (n-r) – линейная комбинация базисных r строк, т.е. эти уравнения можно вычислить как следствие базисных. После этого осталось r линейно независимых строк (уравнений).

минор не равен 0.

Перенесем неизвестные, не входящие в базисный минор направо. Они называются свободными. А те, которые в базисном, x1, x2, …, xr – главные неизвестные.

Если переменным справа придать любые значения, то по правилу Крамера x1, x2, …, xr будут иметь одно однородное определенное значение. Таким образом, можно получить всевозможные решения системы.

=

Если r<n, то система имеет бесконечно много решений, которые можно записать в виде векторных столбцов. А к векторам применима линейная независимость. Согласно линейной независимости векторов, решения будут линейно независимы, когда существует такая их линейная комбинация C1X1+C2X2+…=0, в которой коэффициент C=0.