Экзаменационные вопросы по математике / 13 . - .

Интегрирование рациональных функций. Теорема о разложении дробнорациональной функции на элементарные дроби. Интегрирование элементарных функций

Определение 1. Целой функцией называется многочлен (полином).

Определение 2. Дробно-рациональной функцией называется дробь, числителем и знаменателем которой являются многочлены.

Определение 3. Дробно-рациональная функция называется неправильной рациональной дробью, если степень числителя не меньше степени знаменателя(n m).

Определение 4. Дробно-рациональная функция называется правильной, если степень числителя меньше степени знаменателя.

Теорема: Любую неправильную рациональную дробь можно представить в виде суммы целой функции и правильной рациональной дроби.

Постановка задачи интегрирования дробно-рациональной функции.

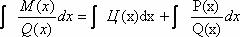- задача свелась к интегрированию правильной рациональной дроби.

Простейшие рациональные дроби.

Простейшими рациональными дробями являются рациональные дроби:

1)

2)

3)

Выделяем полный квадрат и делаем замену переменной:

Тогда интеграл примет вид:

Делаем обратную замену переменной и получаем окончательный ответ. Разложение правильной рациональной дроби на сумму простейших дробей.

Дана правильная дробь:

Теорема 1. Если знаменатель Q(x) имеет любые корни, то правильная дробь разлагается на сумму простейших дробей 1 и 2 типа.

(1)

Интегрирование правильной рациональной дроби.

сумме интегралов от простейших дробей (см. формулу 1 из 9.4).