Экзаменационные вопросы по математике / 26. Ряды с неотрицательными членами. Необходимое и достаточное условие сходимости. Признак сравнения

26. Ряды с неотрицательными членами. Необходимое и достаточное условие сходимости. Признак сравнения.

Положительный ряд сходится тогда и только тогда, когда последовательность его частичных сумм ограничена сверху.

Необходимое условие:

Так как ряд сходится, то последовательность частичных сумм имеет предел. Следовательно она ограничена. А значит она ограничена и снизу и сверху. Доказано Достаточное условие:

Дан положительный ряд и последовательность частичных сумм ограничена сверху. Покажем, что наша последовательность(из членов ряда) неубывающая: S(n + 1) − S(n) = a(n + 1) Теперь используем свойство из теоремы о монотонной последовательности и получим, что последовательность частичных сумм ограничена сверху.

Признак сравнения:

Пусть даны два ряда с положительными членами

и

и каждый член ряда (17) не превосходит соответствующего члена ряда (18), т.е.

выполняется 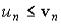(n = 1, 2, 3, …). Тогда, если сходится ряд (18), то сходится и ряд (17). Если ряд (17) расходится, то ряд (18) также расходится. Этот признак остается в

силе, если условие выполняется не для всех n, а лишь начиная с некоторого номера n = N.