Экзаменационные вопросы по математике / 19. Критерий интегрируемости ограниченной на отрезке функции

19. Критерий интегрируемости ограниченной на отрезке функции.

Критерии интегрируемости:

Необходимое условие: функция f должна быть ограниченной на отрезке [a,b].

Критерий Коши:

Для существования неопределенного интеграла необходимо и достаточно, чтобы

Достаточный признак:

Для интегрирования f достаточно.

. Доказательство:

В отрезке

Пусть , тогда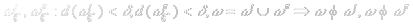

f интегрируемая функция, ч.т.д. Следствие №1:

Если функция f ограничена на [a, b] и имеем на нем конечное число точек разрыва, то функция fинтегрируема на [a, b].

Доказательство:

Пусть f имеет на [a, b] k-точек разрыва

Рассмотрим у каждой точки разрыва с радиусом и вычтем из отрезка

+

выберем , такое, что ;

; {берётся по отрезкам, которые не пересекаются с окрестностью точек разрыва}+{все остальные} < ч.т.д.