Экзаменационные вопросы по математике / 1. Определитель. Определение и свойства. Понятие перестановки

1. Определитель. Определение и свойства. Понятие перестановки. Чётность перестановки. Разложение определителя по элементам строки и столбца.

Определитель (детерминант) А n-ого порядка квадратной матрицы А – называется сумма всевозможных произведений из n элементов матрицы, взятых из каждой строки и каждого столбца со знаком, определяющим выражение (-1)ti+tj, где ti – чётность перестановки из индексов строк, а tj – чётность перестановки из индексов столбцов.

Det A = ∑(-1)ti+tjai1j1*ai2j2*ai3j3*…*ainjn.

Перестановкой из n чисел (элементов) называется упорядоченное расположение этих чисел друг за другом.

Инверсия перестановки – изменение порядка следования (большее число идёт за меньшим).

Если общее число инверсий чётное, то перестановка чётная, а если общее число инверсий нечётное – то перестановка нечётная.

Свойства перестановок:

Взаимное изменение положение 2х элементов перестановки называется транспозицией.

abcd ->dbca

Утверждение: 1 транспозиция меняет чётность перестановки.

1. Соседние – ai1, ai2, …, aik, aij, …, ain -> ai1, ai2, …, aik, aij, …, ain

2. Несоседние - ai1, ai2, …, aik, aik+1, aik+2 ,…, aik +p, …, ain - p соседних транспозиций +p-1 = 2p-1

1

2

3

…

…

n

n(n+1)(n+2)…*1=n! (произведение последовательных натуральных чисел)

Транспозиция несоседних элементов:

Утверждение: Все n! перестановок из n чисел могут быть расположены последовательно друг за другом так, что каждая последующая перестановка получится из предыдущей путём 1 транспозиции.

Доказательство (метод индукции):

1) n=2 – Утверждение верно.

|1 2|

|2 1|

2) Если предположить, что утверждение верно для числа n-1, то из этого следует его справедливость для числа n.

i1,i2,i3,…,in

- зафиксируем 1 элемент и совершим возможные перестановки n-1.

- затем зафиксируем 2 элемент. Осталось n-2 перестановок и т.д.

Из этого следует, что любые 2 перестановки могут быть получены из любой другой конечным числом транспозиций.

n! – всегда чётное число -> если расположить члены друг за другом, то количество чётных перестановок = количеству нечётных.

Вывод: в каждом определителе число отрицательных членов = числу положительных.

Свойства определителей.

Транспонирование не меняет определителя. (Транспонирование – взаимная замена строк и столбцов.)

=

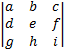Возьмём любой член определителя (-1)ti+tjai1j1*ai2j2*ai3j3*…*ainjn.

Из вида любого члена определителя видно, что при транспонировании они не меняются.

det AT = det A

1. Если в определителе поменять местами 2 строки, то знак определителя поменяется на противоположный.

Доказательство: Берём произвольный член определителя. Взаимное расположение -> поменялись первые 2 индекса -> чётность изменилась -> изменился знак.

2. Если в определителе 2 строки (столбца) одинаковы, то det = 0.

Если 2 одинаковые строки поменять местами, то ничего не меняется, но по св-ву 2 знак меняется. Это происходит, если △=0. (△=-△, 2△=0, △=0)

3. Если в определителе есть 2 пропорциональные строки, то он тоже = 0.

det = k det

после того, как k вынесен, 2 строки равны. По св-ву 3 △ =0.

4. Если в некоторой строке определителя все элементы в виде 1 и той же комбинации чисел, а именно k-я строка (αck1 + βdk1 + αck2+ βdk2) = α|ck1+ck2…+ckn|+β|dk1+dk2…+dkn|.

5. Если в любой строке определителя прибавить любую другую строку с противоположным коэффициентом, то определитель не изменится.

6. Если строка в определителе состоит из нулей, то определитель = 0.

7. Если какая-либо строка определителя есть линейная комбинация других строк, то определитель = 0.

1 = (a11,a1n)

2 = (a21,a2n)

n = (an1,ann)

	1
Det A=	2
	n

Пусть k есть линейная комбинация остальных:

k = α11 + α22 +…+ αk-1k-1 + αk+1k+1 +…+ αnn

В соответствии со свойством 7 определитель равен сумме этих определителей, равных нулю. Количество определителей = (n-1)и в каждой из которых имеются одинаковые строки.

Разложение определителя по элементам строки или столбца.

Минором элемента определителя aik называется определитель n-1 порядка, получающийся вычёркиванием строки и столбца, на пересечении которых стоит элемент aik.

Алгебраическим дополнением Аik элемента определителя aik называется Aik = (-1)i+kMik.

Теорема. Определитель равен сумме произведений элементов какой-либо строки на их алгебраические дополнения.

det A = ak1Ak1+ak2Ak2+…+aknAkn =

1. Доказательство: Пусть определитель имеет вид:

=

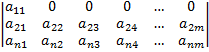a11

Определитель 1 порядка, полученный вычёркиванием 1 строки и 1 столбца.

Тем самым, для 1 случая теорема доказана.

2. Пусть определитель имеет вид:

= (-1)j

an1 an2 an3 an4 … anm

Передвинем последовательными шагами столбец этого элемента akj (столбец с номером j) влево до занятия им места 1 столбца. При этом определитель при каждом шаге меняет знак и итоге приобретает множитель (-1)j и приобретает вид:

anj an1 an2 an3 … anm

Далее перемещаем строку с номером k вверх последовательно, пока она не займёт место 1ой строки, т.е. определитель будет иметь вид:

anj an1 an2 an3 … anm

При этом определитель приобретает ещё один множитель (-1)k. В итоге

anj an1 an2 an3 … anm

Мы пришли к 1 случаю, для которого справедливость была доказана.

det A = (-1)j+kakjMkj+0*Ak1+…+0*Ak2 *…*0*Akn

3. Общий случай.

a11	a12	…	a1m
…	…	…	…
ak1	ak2	…	akm
…	…	…	…
an1	an2	…	anm

=(-1)k+1ak1Mk1+(-1)k+2ak2Mk2+…+(-1)k+naknMkn

Это правило вычисления определителя называется разложением по I строке (столбцу).