Экзаменационные вопросы по математике / 16. Определённый интеграл. Интегральная сумма. Верхние и нижние интегральные суммы. Их свойства. Геометрический смысл оп

16. Определённый интеграл. Интегральная сумма. Верхние и нижние интегральные суммы. Их свойства. Геометрический смысл определённого интеграла.

Пусть на некотором промежутке задана функция . y

разбиения).

Фигура под кривой называется криволинейной трапецией.

- определение определенного интеграла (если предел существует).

Интегральные суммы и их свойства:

Нижняя интегральная сумма: , где Верхняя интегральная сумма: , где 1) , при данном конкретном разбиении.

2) если разбиение получается из разбиения T добавлением одной точки разбиения, то нижняя интегральная сумма может только увеличиться, а верхняя только уменьшиться, т.е.

m'i

mi

Следствие: при добавлении к любому1 разбиению T любого дополнительного числа точек разбиения нижняя интегральная сумма может только увеличиться, а верхняя - только увеличиться.

3)Для любых 2-х разбиений T' и T'', нижняя интегральная сумма любого разбиения не

превосходит интегральную сумму другого разбиения .

Доказательство: по предыдущему свойству рассмотрим разбиение T, полученное из всех

точек разбиения T' и T''. Тогда . Аналогично 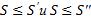. И т.к. , то , что и требовалось доказать.

4)Все нижние интегральные суммы ограничены сверху, а все верхние интегральные суммы ограничены снизу. Как известно, множество чисел, ограниченных сверху имеют

точную верхнюю грань аналогично и для ограниченных снизу - нижняя грань .

-верхняя грань для s.

-верхняя грань для S.

Геометрический смысл определенного интеграла - это площадь фигуры, ограниченной прямыми , осью и графиком функции .