Экзаменационные вопросы по математике / 36. Разложение функций в степенные ряды. Ряд Тейлора. Достаточное условие Разложимости функций в ряд Тейлора

36. Разложение функций в степенные ряды. Ряд Тейлора. Достаточное условие Разложимости функций в ряд Тейлора.

Определение: Пусть . Тогда ряд  называется рядом Тейлора функции  в точке . Если , то  по формуле Тейлора: 

, где  - остаточный член формулы Тейлора, т.е. , где  - n-ая частичная сумма ряда Тейлора функции  в точке .ряд Тейлора сходится на тогда и только тогда, когда  . теор.: Пусть  и    , тогда на   

Доказательство: , где  - остаточный член формулы Тейлора в форме Лагранжа:

   .

Рассмотрим ряд ,  по признаку Даламбера ряд сходится . Перейдем к пределу при  в неравенстве 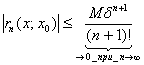    на .