Экзаменационные вопросы по математике / 10. Первообразная функции. Свойства первообразной. Теорема об общем виде первообразной

10. Первообразная функции. Свойства первообразной. Теорема об общем виде первообразной.

Если на некотором промежутке задана функция f(x), а функция F(x) на этом же промежутке дифференцируема и в каждой точке F’(x)=f(x), то функция F(x) называется первообразной для функции f(x) на этом промежутке.

Пример: Предположим, имеется функция: f(x)=, x . Найти F(x). F(x)=arcsinx.

Свойства первообразных:

1) Если F(x) есть первообразная для f(x) на промежутке, тогда F(x)+C тоже первообразная для f(x), где C – произвольная постоянная.

Доказательство: (F(x)+C)’=F(x)’+C’=F’(x)=f(x).

2)Если F(x) – первообразная для f(x) на промежутке, то для функции f(kx+b) (k,b const) первообразной будет функция (1/k)F(kx+b).

Доказательство: ((1/k)F(kx+b))’=(1/k)F’(kx+b)=(1/k)f(kx+b)(kx+b)’=(1/k)f(kx+b)k=f(kx+b).

Свойство линейной замены переменных: Пусть f(x)= , k=3

Найдем первообразную для функции 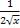, тогда F(x)=, тогда F=1/3 f(x)=, k=-1/x, F=

3) Основное свойство первообразной Две различные первообразные одной и той же функции могут отличаться только на постоянное значение.

Лемма Ла-Гранжа:

Если производная некоторой функции тождественно равна нулю на некотором промежутке, то функция тождественно равна постоянной на этом промежутке.

Доказательство:

Теорема:

Докажем, что первообразная отличается только на const. F1(x)-F2(x)=C. F’1(x)=f(x)

F’2(x)=f(x)

по лемме следует, что , F1(x)-F2(x)=C, ч.т.д.

+C=f(x) – общий вид.