3.3 Экономическое содержание коэффициентов пропорциональности

Рассмотрим двойственную задачу и двойственные оценки. Двойственные оценки позволяют определить ценность ресурса для конкретного предприятия. Если она равна 0, то ресурс является избыточным. Если неравна 0,то дефицитным. Двойственные оценки имеют единицы измерения целевой функции. Для их расчета необходимо составить и решить двойственную задачу. Она является относительно прямой задачи, т.е. она составляется на основании прямой задачи.

Методика составления двойственной задачи:

1. Все ограничения задачи приводим к одному знаку (которого больше). Все известные переносим в левую часть, все неизвестные - в правую.

2. В двойственную задачу вводим столько двойственных оценок, сколько ограничений в прямой задачи. Двойственная оценка обозначается 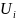, где i-номер ограничения

3. Коэффициенты строки двойственной задачи равны коэффициентам столбца прямой задачи

4. Свободные члены двойственной задачи равны коэффициентам целевой функции прямой задачи

5. Знаки ограничений и цель решения двойственной задачи противоположны по отношению к прямой задачи

6. Коэффициенты целевой функции двойственной задачи равны свободным членам прямой задачи

Решение двойственной задачи осуществляем симплексным методом По результатам решения двойственной задачи можно получить рез-ты реш-я прямой задачи:

• Дополнительные НБП двойственной задачи равны основным переменным прямой задачи и их значения со знаком + берем из целевой функции.

• Небазисные двойственные оценки равны дополнительным переменным прямой задачи и их значение берем из строки целевой функции со знаком +

• БП двойственной задачи соот-ют НБП прямой задачи и равны 0

• Результат решения двойственной задачи равен рез-ту реш-я прямой задачи

Корректировка оптимального решения

Она необходима:

• Если в связи с измененными производ. условиями происходит увеличение или снижение каких-либо ресурсов.

• Если в решение вводятся новые ограничения на определенные ресурсы.

Этапы проведения корректировки:

1. Корректировка по основным небазисным переменным( выбираются основные небазисные переменные, по которым будет проводится корр., например Х1; определяем предельную величину корр. по основной небазисной переменной. Она = минимальному положительному частному от деления свободного члена на коэффициент пропорц. столбца, по которому проводим кор. max ΔXj = min + (bi/aij); задаем новое условие, проводим кор. по основной формуле xj^k(yi^k) = xj(yi) – aij*Δxj(Δyi), Δxj>0 ).

2. Корректировка по основным небазисным переменным, если ресурсы уменьшаются Δyi>0 ( определяем дополнительную небазисную переменную, по которой будем проводить корректировку, т.е. определяем, какой из ресурсов будет снижаться(y1); определяем предельную величину корректировки = минимальному положительному частному от деления свободного члена на коэффициент пропорциональности столбца, по которому проводится корректировка max Δyi = min + (bi/aij); новое условие( с экономической точки зрения предельная величина корректировки показывает на сколько можно снизить данный ресурс и при этом получить оптимальное решение, используя коэффициент пропорциональности и не решая задачу вновь).

3. Корректировка оптимального решения по дополнительным небазисным переменным, если ресурсы увеличиваются, т.е. Δуi<0 ( выбираем, какой из ресурсов будет увеличиваться, т.е. выбираем переменную, по которой будем проводить корректировку; определяем предельную величину корректировки по выбору переменной, она равна минимальному по абсолютной величине отрицательному частному от деления свободных членов на коэффициент пропорциональности столбца, по которому проводим корректировку maxΔyi = min | - (bi/aij)|, получено оптимальное решение; сравниваем требуемую и предельные величины корректировки и делаем вывод о возможности проведения корректировки.