2.4.Модели с качественными переменными

В большинстве случаев рассматриваются регрессионные модели, в которых факторы имеют количественное значение, однако на практике возникает необходимость исследовать влияние качественных признаков.

Все качественные признаки делят на 2 группы:

• Альтернативные

• Нарастающие

Нарастающие изменяются от какой-то величины и возрастают. Они формируются под влиянием нескольких элементов, взаимодействующих между собой. Взаимосвязь чаще всего нелинейная, поэтому вывести формулу оценки нарастающего качественного признака сложно.

Качественные альтернативные признаки характер-ся тем, что они присутствуют или нет.

Чтобы ввести качественные переменные в регрессионную модель им должны быть присвоены цифровые метки, т.е. качест. Переменные преобразованы в количественные. Такие сконструированные переменные наз-ся фиктивными (структурными). В качественных фиктивных переменных обычно используют бинарные переменные, которые принимают 2 значения: присутствует (1), отсутствует (0)

3.1 Необходимость математических методов и моделей в условиях рынка

Экономико- математическое моделирование объед. Этап познания сущности объекта, его причина следственных связей, количественное описание его наиболее важных существенных сторон функционирования, построения и решения экономико-математических задач и механизм реализации получения оптимального решения.

Экономико-математическая модель – система уравнений или неравенств, описывающая наиболее существенные стороны функционирования экономическаого объекта.

Построение и решение экономико-математич. моделей назыв. экономико-математическим моделированием.

Решение эк-мат. Задач осуществляется с помощью математич. методов.

Мат. Метод представляет собой программу вычислений обеспечивающую нахождение лучшего варианта решения задачи, условия которой заданы количественно.

Мат. методы:

1. Оптимальные (Симплексный метод – опубликован в 1949 г. Данцигом, в 40-е гг. Конторович)

2. Неоптимальные (Метод Фогеля позволяет получать решения близкие к оптимальным)

По своим возможностям мат. методы делятся на группы:

а) универсальные, кот. позволяют решать задачи любого типа(симплексный метод)

б) специальные, позвол. Решить задачи определенного типа (задачи транспортного характера решаются методом потенциалов)

Нобелевские премии по экономике получили экономисты- математики:

Ян Тильберген (1969)

Лоуренс Клей (1980)

Трюгве Хаавельмо (1989)

Джеймс Хекман, Дэниэль Мак-Фадден (2000)

3.2 Сущность идеи симплексного метода.

Симплексный метод является универсальным, т.к. позволяет решать задачи, условия которых выражены в различных единицах измерения и заданы в виде уравнений и неравенств.

Этапы симплексного метода:

1. Преобразуем ограничения в неравенства

1. Переносим все независимые в первую часть неравенств, все известные во вторую часть, приводим все ограничения к знаку

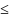
2. Все неравенства преобразуем в уравнения, вводя в каждое ограничение дополнительную переменную , где 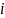- номер ограничения

Экономический смысл : в ограничениях обозначает недоиспользование ресурсов, а в ограничениях 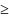обозначает величину превышения максимальной границы

2. Условие задачи заносим в 1-ю симплексную таблицу, причем коэффициенты целевой строки заносим с противоположным знаком

3. Поиск опорного решения – если все коэффициенты столбца свободных членов положительные и нет 0 среди базисных переменных

Поиск разрешающего элемента (опорное решение отсутствует):

• В столбце свободных членов находится отрицательный, если их несколько берем любой

• В строке выбранного отрицательного свободного члена находим отрицательный коэффициент, если их несколько берем любой

• Путем деления коэффициентов столбца свободных членов на коэффициенты столбца с выбранным отрицательным элементом, находим положительные значения, среди которых выбираем наименьшее. Оно и показывает, где будет разрешающий коэффициент. Разрешающий коэффициент показывает, какая из небазисных переменных заменяет базисную.

• Правила нахождения нов.эл. в синт.табл.: на месте разреш-го эл. Записываем обратную величину(1:-1=-1) ; новые эл.разреш.строки находим делением(-50:-1=50); новые эл.разреш.столбца находим делением старых элементов на разрешающих взятый с противоположн.знаком(0:+1=0; 5:+1=+5; 1:1=1). Все остальные эл.находим по праввилу прямоугольника: от произведения элементов гл.диогонали (содержит разреш.эл) отнимаем произведение эл-ов побочной диогонали и полученный результат делим на разреш.элемент. Примечание: если произведение эл.побочной диагонали=0,эл остается без изменений. Если произвед.гл.диогонали=0, то вычесление произведений необходимо.

4. Поиск оптимального решения. Признак оптим-го реш-я: если коэф.целевой ф-ции будут положит. При решении задачи на max или отриц.при реш.задачи на min.

Поиск разрешающего элемента (опорное решение найдено).

• среди коэф.целевой строки выбираем несоответствующее правилам оптимальности. Среди них выбираем наибольший по модулю. Он указывает на разреш.столбец.

• делим столбец СЧ на разреш.столбец. Среди полученных частных выбираем наименьшее положит.чостное, кот.указывает на разреш.строку.

• на пересечении разреш.столбца и строки находим разрешающий эл.

Оптимальное решение получено,когда все коэф.целевоц строки при решении на max явл.положит-ми(на min - отрицательные). Все БП=СЧ, а НБП=0