Интегрирование по частям.

Метод интегрирования по частям позволяет свести исходный неопределенный интеграл к более простому виду либо к табличному интегралу. Этот метод наиболее часто применяется, если подынтегральная функция содержит логарифмические, показательные, обратные тригонометрические, тригонометрические функции, а также их комбинации.

Формула интегрирования по частям следующая .

То есть, подынтегральное выражение f(x)dx представляем в виде произведения функции u(x) на d(v(x)) - дифференциал функции v(x). Далее находим функцию v(x) (чаще всего методом непосредственного интегрирования) и d(u(x)) - дифференциал функции u(x). Подставляем найденные выражения в формулу интегрирования по частям и исходный неопределенный интеграл сводится к разности . Последний неопределенный интеграл может быть взят с использованием любого метода интегрирования, в том числе и метода интегрирования по частям.

В качестве примера найдем множество первообразных функции логарифма.

Пример.

Найти неопределенный интеграл

Решение.

Найдем этот неопределенный интеграл методом интегрирования по частям. В качестве функции u(x) возьмем ln(x), а в качестве d(v(x)) оставшуюся часть подынтегрального выражения, то есть dx.

Имеем, , где .

Дифференциал функции u(x) есть , а функция v(x) – это .

ЗАМЕЧАНИЕ: константу С при нахождении функции v(x) считают равной нулю.

Теперь все подставляем в формулу интегрирования по частям:

Ответ:

.

Самое сложное, что есть в этом методе – это правильно определить, какую часть подынтегрального выражения брать за u(x), а какую за d(v(x)).

Рассмотрим стандартные случаи.

• Для интегралов вида или , где - многочлен степени n, a – коэффициент, в качестве функции u(x) выбираем многочлен .

Пример.

Найти множество первообразных функции .

Решение.

Неопределенный интеграл можно взять методом интегрирования по частям.

В качестве функции u(x) следует взять x+1, тогда d(v(x)) = sin(2x)dx.

Следовательно, d(u(x)) = d(x+1) = dx, а с помощью непосредственного интегрирования получаем .

Выполняем подстановку в формулу интегрирования по частям:

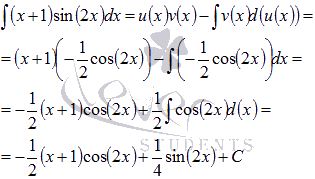
Ответ:

.

Пример.

Найти неопределенный интеграл .

Решение.

В качестве функции u(x) нужно взять многочлен второго порядка , тогда .

К полученному интегралу вновь применим метод интегрирования по частям:

Ответ:

.

Пример.

Найти интеграл .

Решение.

Используем метод интегрирования по частям. Пусть , а . Тогда , а . Подставляем в формулу:

Пришли к неопределенному интегралу, который также возьмем по частям:

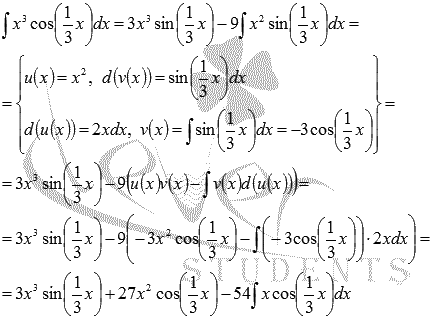
И еще раз интегрируем по частям:

Ответ:

.

• Для интегралов вида , или , в качестве функции u(x) выбираем функции ln(ax), arcsin(ax), arcos(ax), arctg(ax) и arcctg(x) соответственно.

Пример.

Найдите множество первообразных функции .

Решение.

При интегрировании по частям примем u(x) = ln(2x), d(v(x)) = (x+1)dx, тогда и . Подставляем в формулу интегрирования по частям:

Ответ:

.

Пример.

Найти неопределенный интеграл .

Решение.

Используем метод интегрирования по частям. В качестве функции u(x) возьмем arcsin(2x), d(v(x)) = xdx, тогда .

Применяем формулу:

Таким образом, пришли к равенству:

Найдем отдельно полученный интеграл .

Применим метод интегрирования по частям:

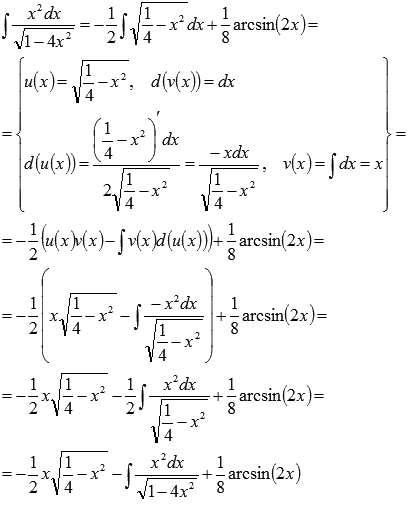
Таким образом, получили равенство .

Интеграл в правой части равенства получился таким же как и в левой части. Перенесем его из правой части в левую:

Теперь можно возвращаться к началу примера:

Ответ:

.

• Для интегралов вида или в качестве функции u(x) выбираем любую из функций.

Пример.

Найти неопределенный интеграл .

Решение.

Что мы имеем в итоге:

Интегралы в левой и правой частях равенства совпадают, поэтому можно привести подобные слагаемые:

Это стандартный метод для таких задач, и при интегрировании по частям не редко в правой части получается интеграл, совпадающий по виду с исходным.

В других случаях, какую часть подынтегрального выражения брать за функцию u(x), а какую за d(v(x)) выявляется методом проб и ошибок.