файл – Сопромат. rtf

Тестовый материал по сопротивлению материалов

на 2009/20010 учебный год

Специальность: 110304 - Технология обслуживания

и ремонта машин в АПК, 110301 – Механизация сельского хозяйства

Разработчик тестов – Коваленко А.Е.

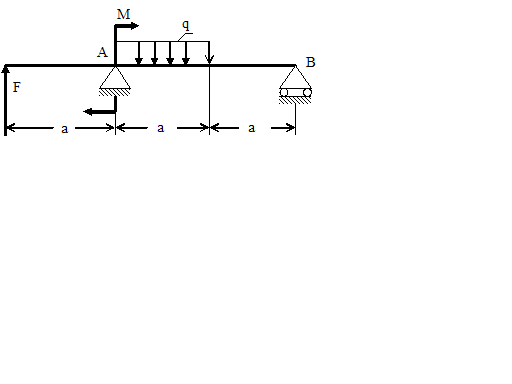
1. Запишите уравнение углов поворота для первого участка балки.

а) ;

+б) ;

в) ;

г) ;

д) .

2. Запишите уравнение прогибов для первого участка балки.

+а) ЕJ ;

б) ЕJ ;

в) ЕJ ;

г) ЕJ ;

д) ЕJ .

3. Запишите уравнение углов поворота для первого участка балки.

а) ЕJ ;

+б) ЕJ ;

в) ЕJ ;

г) ЕJ ;

д) ЕJ .

4. Запишите уравнение прогибов для первого участка балки.

а) ЕJ ;

б) ЕJ ;

в) ЕJ ;

г) ЕJ ;

+д) ЕJ .

5. Запишите уравнение углов поворота для 1 участка.

а) ЕJ ;

б) ЕJ ;

в) ЕJ ;

+г) ЕJ ;

д) ЕJ .

6. Запишите аналитическое выражение изгибающего момента для первого участка балки.

а) М(u)= ;

б) М(u)= ;

в) М(u)= ;

+г) М(u)= ;

д) М(u)= .

7. Запишите выражение изгибающего момента.

а) М(u)= ;

б) М(u)= ;

в) М(u)= ;

+г) М(u)= ;

д) М(u)= .

8. Запишите выражение изгибающего момента.

а) М(u)= ;

б) М(u)= ;

+в) М(u)= ;

г) М(u)= ;

д) М(u)=

9. Запишите выражение изгибающего момента.

а) М(u)= ;

б) М(u)= ;

+в) М(u)= ;

г) М(u)= ;

д) М(u)= .

10. Запишите аналитическое выражение изгибающего момента.

а) М(u)= ;

б) М(u)= ;

в) М(u)= ;

+г) М(u)= ;

д) М(u)= .

11. Запишите аналитическое выражение изгибающего момента.

а) М(u)= ;

б) М(u)= ;

в) М(u)= ;

+г) М(u)= ;

д) М(u)= .

12. Определите площадь эпюры изгибающего момента от всей заданной внешней нагрузки, если q = 10 кН/м; = 2 м. .

а) 13 кН·м;

+б) 40/3 кН·м;

в) 15 кН·м;

г) 50/3 кН·м;

д) 21 кН·м.

13. Определите площадь эпюры изгибающего момента от всей заданной внешней нагрузки, если М = 20 кН·м; F = 10 кН.

а) 30 кН·м²;

+б) 40 кН·м²;

в) 20 кН·м²;

г) 35 кН·м²;

д) 15 кН·м².

14. Определите площадь эпюры изгибающего момента от всей заданной внешней нагрузки, если М = 20 кН·м.

+а) 10 кН·м²;

б) 20 кН·м²;

в) 7,5 кН·м²;

г) 15 кН·м²;

д) 25 кН·м².

15. Определите площадь эпюры изгибающего момента от всей заданной внешней нагрузки, если F = 10 кН.

а) 10 кН·м²;

+б) 20 кН·м²;

в) 15 кН·м²;

г) 5 кН·м²;

д) 25 кН·м².

16. Определите площадь эпюры изгибающего момента от всей заданной внешней нагрузки, если М = 20 кН·м; F = 10 кН.

а) 20 кН·м²;

б) 15 кН·м²;

+в) 25 кН·м²;а

г) 40 кН·м²;

д) 30 кН·м².

17. Определите площадь эпюры изгибающего момента от всей заданной внешней нагрузки, если М = 20 кН·м; F = 10 кН.

а) 10 кН·м²;

+б) 15 кН·м²;

в) 25 кН·м²;

г) 30 кН·м²;

д) 5 кН·м².

18. Определите площадь эпюры изгибающего момента от всей заданной внешней нагрузки, если q = 10 кН/м; = 2 м; М = 20 кН·м; F = 10 кН.

а ) 15 кН·м²;

б) 10 кН·м²;

+в) 20/3 кН·м²;

г) 40/3 кН·м²;

д) 25/3 кН·м².

19. Как записывается условие прочности при изгибе.

а) ;

+б) ;

в) ;

г) ;

д) .

20. Как записывается условие жесткости при изгибе.

а) ;

б) ;

в) ;

г) ;

+д) .

21. Как определяется минимальный радиус инерции.

а) ;

б) ;

в) ;

+г) ;

д) .

22. Чему равен коэффициент приведения длины стержня, если один его конец защемлен, а второй свободный.

а) 1;

б) 2;

в) 0,5;

+г) 0,7.

23. Какой цикл переменных напряжений будет симметричным.

а) ;

б) ;

в) ;

г) ;

+д)

24. Какой цикл переменных напряжений будет отнулевым.

+а) ;

б) ;

в) ;

г) ;

д) .

25. Подобрать номер двутавра для балки нагруженной силой F, если силовая линия составляет с главной осью инерции угол =30⁰; МПа.

а) I № 24;

+б) I № 27;

в) I № 20;

г) I № 30;

д) I № 33.

26. Подобрать номер двутавра для балки погруженной силой F, если силовая линия составляет с главной осью инерции угол =30⁰; МПа.

а) I № 20;

б) I № 36;

в) I № 45;

+г) I № 50;

д) I № 55.

27. Подобрать номер двутавра для балки нагруженной моментом М, если силовая линия составляет с главной осью инерции угол =30⁰; МПа.

а) I № 40;

+б) I № 36;

в) I № 27;

г) I № 45;

д) I № 50.

28. Подобрать номер двутавра, если силовая линия составляет с главной осью инерции угол =30⁰; МПа.

а) I № 36;

б) I № 40;

в) I № 45;

+г) I № 50;

д) I № 55.

29. Подобрать номер двутавра для балки погруженной силой F, если силовая линия составляет с главной осью инерции угол =30⁰; МПа.

а) I № 40;

+б) I № 36;

в) I № 27;

г) I № 50;

д) I № 40.

30. Определите диаметр вала по четвертой теории прочности, если .

+а) 160 мм;

б) 165 мм;

в) 155 мм;

г) 150 мм;

д)145 мм.

31. Определите диаметр вала по четвертой теории прочности, если .

а) 175 мм;

+б) 180 мм;

в) 170 мм;

г) 150 мм;

д) 185 мм.

32. Определите положение нейтральной оси для прямоугольного сечения

а)

б)

+в)

г)

д)

33. Определите положение нейтральной оси для прямоугольного сечения

а)

б)

+в)

г)

д)

34. Определите положение нейтральной оси для прямоугольного сечения

а)

б)

+в)

г)

д)

35. Какое максимальное напряжение возникает в прямоугольном сечении балки, если высота сечения:

а)

б)

+в)

г)

д)

36. Какое максимальное напряжение возникает в прямоугольном сечении балки, если высота сечения:

а)

б)

в)

+г)

д)

37. Определите минимальный радиус инерции для круглого сечения диаметром d.

а)

+б)

в)

г)

д)

38. Определите минимальный радиус инерции для прямоугольного сечения с размерами сторон .

+а)

б)

в)

г)

д)

39. Определите минимальный радиус инерции для прямоугольного сечения с размерами сторон .

а)

+б)

в)

г)

д)

40. Определите минимальный радиус инерции для квадратного сечения с отверстием диаметром а.

+а)

б)

в)

г)

д)

41. Определите минимальный радиус инерции для полого квадрата с толщиной стенки 0,2 а.

+а) 0,337 а;

б) 0,289 а;

в) 0,364 а;

г) 0,264 а;

д) 0,114 а.

42. Определите критическую силу для стального стержня круглого поперечного сечения, если оба его конца закреплены шарнирно диаметр d=80 мм, длина.

м.

а) 880 кН;

+б) 992 кН;

в) 844 кН;

г) 756 кН;

д) 1102 кН.

43. Определите критическую силу для стального стержня круглого поперечного сечения, если оба его конца защемлены, диаметр d=80 мм, длина.

м.

а) 1421 кН;

б) 1532 кН;

+в) 1271 кН;

г) 1200 кН;

д) 1325 кН.

44. Определите критическую силу для стального стержня круглого поперечного сечения, если оба его конца закреплены шарнирно диаметр d=100 мм, длина.

м.

а) 1200 кН;

+б) 1720 кН;

в) 1840 кН;

г) 2020 кН;

д) 1890 кН.

45. Определите критическую силу для квадратного стержня, со стороной сечения а=100 мм, если оба его конца защемлены, а длина =1,8 м, материал стержня Ст3.

+а) 2740 кН;

б) 2850 кН;

в) 2630 кН;

г) 2160 кН;

д) 2220 кН.

46. Определите критическую силу круглого стержня, если один конец стержня защемлен, а второй свободный, d=100 мм, =2,5 м, материал стержня Ст3.

а) 390 кН;

+б) 387 кН;

в) 400 кН;

г) 420 кН;

д) 464 кН.

47. По какой формуле определяется коэффициент Пуассона.

а) ;

б) ;

+в) ;

г) .

48. Укажите формулу для определения модуля сдвига.

а) ;

б) ;

в) ;

+г) .

49. Как определяется напряжение при изгибе.

а) ;

+б) ;

в) ;

г) .

50. Чему равен осевой момент инерции Jx.

а) 12 см⁴ ;

+б) 16см⁴;

в) 32см⁴;

г) 8 см⁴;

д) 64см⁴.

51. Как записывается закон Гука при чистом сдвиге.

+а)

б) ;

в) ;

г)

52. Как записывается формула Журавского для определения касательных напряжений.

а) ;

б) ;

в)

+г) ;

д) .

53. По какой формуле определения осевой момент сопротивления изгибу.

а) ;

б) ;

в) ;

+г) ;

д) .

54. Определите гибкость квадратного стержня а = 100 мм, если оба его конца закреплены шарнирно, а длина 2,0 м.

а) 70,1;

+б) 69,2;

в) 70,8;

г) 138, 4;

д) 48,4.

55. При осевом растяжении (сжатии) в поперечном сечении бруса возникают

+а) продольная сила;

б) поперечная сила;

в) крутящий момент;

г) изгибающий момент;

д) крутящий и изгибающий момент.

56. При кручении бруса в его поперечных сечениях возникают

а) продольная сила;

б) поперечная сила;

+в) крутящий момент;

г) изгибающий момент;

д) крутящий и изгибающий момент.

57. При срезе (сдвиге) в поперечных сечениях бруса возникают

а) продольная сила;

+б) поперечная сила;

в) крутящий момент;

г) изгибающий момент;

д) крутящий и изгибающий момент.

58. При чистом прямом изгибе в поперечных сечениях бруса возникают

а) продольная сила;

б) поперечная сила;

в) крутящий момент;

+г) изгибающий момент;

д) крутящий и изгибающий момент.

59. При поперечном прямом изгибе в поперечных сечениях бруса возникают

а) продольная сила;

+б) поперечная сила и изгибающий момент;

в) крутящий момент;

г) изгибающий момент;

д) крутящий и изгибающий момент.

60. При чистом косом изгибе в поперечных сечениях бруса возникают

+а) два изгибающих момента;

б) две поперечные силы;

в) изгибающий и крутящий момент;

г) изгибающий момент и поперечная сила;

д) продольная сила и изгибающий момент.

61. При поперечном косом изгибе в поперечных сечениях бруса возникают

+а) два изгибающих момента и поперечная сила;

б) две поперечные силы;

в) изгибающий и крутящий момент;

г) изгибающий момент и поперечная сила;

д) продольная сила и изгибающий момент.

62. При совместном действии изгиба и кручения в поперечных сечениях бруса возникают

а) два изгибающих момента и поперечная сила;

б) две поперечные силы;

+в) изгибающий и крутящий момент;

г) изгибающий момент и поперечная сила;

д) продольная сила и изгибающий момент.

63. При совместном действии изгиба и осевого растяжения (сжатия) в поперечных сечениях бруса возникают

а) два изгибающих момента и поперечная сила;

б) две поперечных силы;

в) изгибающий и крутящий момент;

г) изгибающий момент и поперечная сила;

+д) продольная сила и изгибающий момент.

64. При внецентренном растяжении (сжатии) в поперечных сечениях бруса возникают

а) два изгибающих момента и поперечная сила;

б) две поперечных силы;

в) изгибающий и крутящий момент;

г) изгибающий момент и поперечная сила;

+д) продольная сила и два изгибающих момента.

65. При осевом растяжении (сжатии) в поперечных сечениях бруса возникают

+а) только нормальные напряжения;

б) только касательные напряжения;

в) нормальные и касательные напряжения.

66. При кручении бруса в его поперечных сечениях возникают

а) только нормальные напряжения;

+б) только касательные напряжения;

в) нормальные и касательные напряжения.

67. При срезе (сдвиге) в поперечных сечениях бруса возникают

а) только нормальные напряжения;

+б) только касательные напряжения;

в) нормальные и касательные напряжения.

68. При чистом прямом изгибе в поперечных сечениях бруса возникают

+а) только нормальные напряжения;

б) только касательные напряжения;

в) нормальные и касательные напряжения.

69. При поперечном прямом изгибе в поперечных сечениях бруса возникают

а) только нормальные напряжения;

б) только касательные напряжения;

+в) нормальные и касательные напряжения.

70. При совместном действии изгиба и кручения в поперечных сечениях бруса возникает

а) только нормальные напряжения;

б) только касательные напряжения;

+в) нормальные и касательные напряжения.

71. При внецентренном растяжении (сжатии) в поперечных сечениях бруса возникают

+а) только нормальные напряжения;

б) только касательные напряжения;

в) нормальные и касательные напряжения.

72. На двух взаимно перпендикулярных площадках касательные напряжения

а) равны по величине и одинаковы по знаку;

+б) равны по величине и противоположны по знаку;

в) не равен по величине и по знаку.

73. При сжатии образцы из хрупких материалов (бронза, чугун)

+а) разрушаются под углом 45⁰;

б) не разрушаются;

в) разрушаются под углом 30⁰;

г) разрушаются произвольно.

74. При сжатии образцы из пластичных материалов (сталь, медь)

а) разрушаются под углом 45⁰;

+б) не разрушаются;

в) разрушаются под углом 30⁰;

г) разрушаются произвольно.

75. С увеличением длины стержня его гибкость

+а) увеличится;

б) уменьшится;

в) не изменится.

76. При изгибе балки нормальные напряжения

а) равномерно распределяются по сечению;

+б) будут максимальными на ее поверхности;

в) будут максимальными на ее оси.

77. Какой стержень обладает большей жесткостью при растяжении (сжатии)

+а) стальной;

б) чугунный;

в) бронзовый;

г) алюминиевый;

д) деревянный.

78. Какое сечение вала является рациональным при кручении

а) сплошное;

+б) полое.

79. С увеличением нагрузки модуль нормальной упругости Е

+а) не изменяется;

б) увеличивается;

в) уменьшается.

80. Чему равен центробежный момент инерции для швеллера № 10

+а) 0;

б) 174 см⁴;

в) 34,8 см³;

г) 20,4 см³;

д) 10,9 см².

81. Чему равен центробежный момент инерции для двутавра № 20

+а) 0;

б) 1840 см⁴;

в) 184 см³;

г) 26,4 см²;

д) 115 см⁴.

82. Какое из главных напряжений следует обозначать σ₁

а) 20 МПа;

б) 40 МПа;

+в) 100 МПа;

г) 0;

д) 5 МПа.

83. Какое из главных напряжений следует обозначать σ₃

а) 20 МПа;

б) 40 МПа;

в) 100 МПа;

+г) 0;

д) 5 МПа.

84. Укажите единицу измерения радиуса инерции

+а) мм;

б) мм²;

в) мм³;

г) мм⁴;

д) безразмерная величина.

85. Укажите единицу измерения гибкости стержня 

а) мм;

б) мм²;

+в) безразмерная величина;

г) мм³;

д) мм⁴.

86. Укажите единицу измерения осевого момента инерции сечения

а) мм;

б) мм²;

в) мм³;

+г) мм⁴;

д) безразмерная величина.

87. Установите величину коэффициента запаса прочности, если σ_т=200 МПа, а [σ]=100 МПа

+а) 2,0;

б) 0,5;

в) 0,6;

г) 4,0;

д) 0.

88. Установите коэффициент запаса устойчивости, если критическая сила F_кр=400 кН, а действующая нагрузка F=200 кН

+а) 2,0;

б) 2,5;

в) 0,55;

г) 0;

д) 3,0.

89. Какое из главных напряжений следует обозначать σ₂

а) 20 МПа;

б) 40 МПа;

+в) 0;

г) -30МПа;

д) -60 МПа.

90. Какую форму имеет ядро сечения для круглого сечения

+а) круг;

б) квадрат;

в) прямоугольник;

г) ромб.

91. Какую форму имеет ядро сечения для прямоугольного сечения

а) круг;

б) квадрат;

в) прямоугольник;

+г) ромб.

92. Как проходит нейтральная ось при косом изгибе

+а) через центр тяжести сечения;

б) параллельно оси бруса;

в) совпадает с главными осями инерции сечения;

г) перпендикулярно внешней нагрузки.

93. С увеличением длины стержня напряжение от собственного веса

+а) увеличится;

б) не изменяется;

в) уменьшится.

94. С увеличением размеров прокатного профиля прогиб балки

а) увеличится;

б) не изменяется;

+в) уменьшится.

95. С увеличением высоты падения груза динамический коэффициент

+а) увеличится;

б) не изменяется;

в) уменьшится.

96. Укажите величину допускаемого напряжения [σ], если σ_т=240 МПа, коэффициент запаса прочности n=2

а) 220 МПа;

+б) 120 МПа;

в) 140 МПа;

г) 500 МПа;

д) 540 МПа.

97. Для увеличения жесткости конструкции брус прямоугольного сечения необходимо установить

+а) на ребро;

б) плашмя.

98. Определите напряжение в сечении стержня, если F=1000 Н, А=20 мм²

+а) 50 МПа;

б) 20·10⁴ МПа;

в) 40 МПа;

г) 80 МПа;

д) 100 МПа.

99. Определите площадь поперечного сечения стержня, если [σ]=10 МПа, F=2000 Н

+а) 200 мм²;

б) 20 мм²;

в) 210 мм²;

г) 180 мм²;

д) 2000 мм².

100. С уменьшением длины стержня его устойчивость

+а) увеличится;

б) уменьшится;

в) не изменится.

101. Если свободный конец стержня заменить жесткой заделкой, его гибкость

а) увеличится;

+б) уменьшится;

в) не изменится.

102. Если диаметр стержня уменьшить в два раза, то его удлинение

а) не изменится;

б) увеличится в 8 раз;

+в) увеличится в 4 раза;

г) уменьшится в 2 раза;

д) уменьшится в 6 раз.

103. Напряжение, при котором наблюдается рост деформаций без изменения нагрузки, называется

а) пределом пропорциональности;

+б) пределом текучести;

в) пределом прочности;

г) критическим;

д) допускаемым.

104. Максимальное напряжение, предшествующее разрушению образца называется

а) пределом пропорциональности;

б) пределом текучести;

+в) пределом прочности;

г) критическим;

д) допускаемым.

105. Напряжение, до которого выполняется закон Гука при осевом растяжении (сжатии) называется

+а) пределом пропорциональности;

б) пределом текучести;

в) пределом прочности;

г) критическим;

д) допускаемым.

106. Способность конструкции сопротивляться деформации называется

а) прочностью;

б) устойчивостью;

+в) жесткостью;

г) изотропностью;

д) выносливостью.

107. Нагрузка, при которой конструкция теряет первоначальную форму равновесия, называется

а) предельной;

+б) критической;

в) динамической;

г) разрушающей;

д) допускаемой.

108. Способность конструкции сопротивляться разрушению называется

+а) прочностью;

б) устойчивостью;

в) жесткостью;

г) изотропностью;

д) выносливостью.

109. Если в элементах конструкций возникают значительные ускорения, то они испытывают нагрузку

а) статическую;

+б) динамическую;

в) критическую;

г) предельную;

д) допускаемую.

110. Изменение формы и размеров тела под действием внешней нагрузки называется

а) перемещением;

+б) деформацией;

в) ползучестью;

г) релаксацией;

д) текучестью.

111. Изменение положения одного и того же элемента конструкций до и после приложения нагрузки называется

+а) перемещением;

б) деформацией;

в) ползучестью;

г) релаксацией;

д) текучестью.

112. Какой материал обладает меньшим значением модуля нормальной упругости

а) сталь;

б) бронза;

в) медь;

г) чугун;

+д) древесина.

113. Главными называют площадки, на которых

+а) отсутствуют касательные напряжения;

б) действуют нормальные и касательные напряжения;

в) действуют только касательные напряжения.

114. На площадках чистого сдвига возникают напряжения

+а) касательные;

б) нормальные;

в) предельные;

г) допускаемые;

д) критические.