19. Фиктивная переменная

 (англ. dummy variable) — качественная переменная, принимающая значения 0 и 1, включаемая в эконометрическую модель для учёта влияния качественных признаков и событий на объясняемую переменную. При этом фиктивные переменные позволяют учесть влияние не только качественных признаков принимающих два, но и несколько возможных значения. В этом случае добавляются несколько фиктивных переменных. Фиктивная переменная может быть также индикатором принадлежности наблюдения к некоторой подвыборке. Последнее можно использовать для обнаружения структурных изменений.

Сформулируем методику построения модели с фиктивными переменными:

1. Разбиваем статистические данные на категории, число которых определяется числом градаций качественного признака. Одну из категорий принимаем за эталонную (выбирается произвольно).

2. Вводим фиктивные переменные для всех категорий, кроме эталонной. Каждая из введенных фиктивных переменных принимает значение, равное единице для данных рассматриваемой категории и нуль для данных остальных категорий.

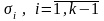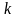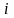3. Фиктивные переменные вводятся в уравнение с коэффициентом , где - число категорий. Каждый из коэффициентов характеризует сдвиг значения результативного показателя для данных - ой категории относительно эталонной. Если оказывается статистически значимым, то фактор (событие), выражаемое этой фиктивной переменной оказывает существенное влияние на результативный показатель.

Модель может содержать несколько качественных признаков. В этом случае фиктивные переменные для каждого признака вводятся в соответствии с вышеприведенной методикой

20. Понятие мультиколлинеарности

Одной из проблем при построении эконометрических моделей является мультиколлинеарность. Под мультиколлинеарностью понимается линейная взаимосвязь двух или нескольких объясняющих переменных. Если переменные взаимосвязаны строго функционально, то имеем дело с совершенной (рис. 2,а) мультиколлинеарностью. В действительности можно столкнуться с очень высокой (рис. 2,б) или близкой к ней мультиколлинеарностью – сильной корреляционной зависимостью между переменны-ми – факторами.

Рис. 2. Мультиколлинеарность явлений. Следует выделить несколько признаков, по которым может быть установлено наличие мультиколлинеарности. 1. Коэффициент детерминации (R2) достаточно высок, но некоторые из коэффициентов регрессии статистически незначимы, т.е. имеют низкую t-статистику. 2. Парная корреляция между малозначимыми переменными достаточно высока. Однако данный признак будет надежным лишь в случае двух объясняющих переменных. При большом их количестве более целесообразным является использование частных коэффициентов корреляции. 3. Высокие частные коэффициенты корреляции. Частные коэффициенты корреляции определяют силу линейной зависимости между двумя переменными без учета влияния на них других переменных. Ниже приведены методы устранения мультиколлинеарности.

Ниже приведены методы устранения мультиколлинеарности. 1. Исключение переменных из модели. 2. Получение дополнительных данных или новой выборки. 3. Изменение спецификации модели (формы модели изменяется, добавляются переменные). 4. Преобразование переменных.

21.Использование критерия Фишера в многофакторных регрессионных моделяхВыполняется сравнение Fфакт и критического (табличного) Fтабл значений F-критерия Фишера. Если табличное значение меньше фактического, то признается статистическая значимость и надежность характеристик, если наоборот, то признается статистическая незначимость, ненадежность уравнения регрессии

Общий F-критерий проверяет гипотезу о статистической значимости уравнения регрессии. Анализ выполняется при сравнении фактического и табличного значения F-критерия Фишера.

Частные F-критерии оценивают статистическую значимость присутствия факторов в уравнении регрессии, оценивают целесообразность включения в уравнение одного фактора после другого.