13. Нелинейные модели регрессии и линеаризация
Различают два класса нелинейных регрессионных моделей:
- модели, нелинейные относительно фактора, но линейные по параметрам;
- модели нелинейные по параметрам.
Модели, нелинейные относительно факторов, но линейные по параметрам. Введением новых переменных такую модель можно свести к линейной, для оценки параметров которой используется обычный метод наименьших квадратов.
Рассмотрим примеры линеаризующих преобразований:
1)
Полиномиальная модель:
.
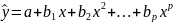Соответствующая
линейная модель:
,
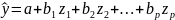где
.
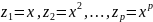2)
Гиперболическая модель:
.
Соответствующая
линейная модель:
,
где
.
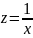3)
Логарифмическая модель:
.
Соответствующая
линейная модель:
,
где
.
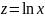Полиномами второго порядка описывается зависимость урожайности от количества внесенных удобрений. Гиперболическая модель может быть использована для характеристики связей между нормой безработицы и процентом прироста заработной платы (кривая Филлипса). Логарифмическая модель может быть использована для описания доли расходов на товары длительного пользования (кривая Энгеля) в зависимости от общих сумм расходов.
Модели нелинейные по параметрам. Среди таких моделей выделяют нелинейные модели внутренне линейные и нелинейные модели, внутренне нелинейные. Модели внутренне линейные можно привести к линейному виду с помощью соответствующих преобразований.
Примеры внутренне линейных моделей и их линеаризация:
1)
Мультипликативная степенная модель:
.
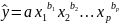Линеаризующее преобразование:
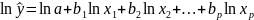
или
,
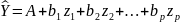где
.
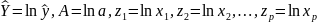2)
Экспоненциальная модель:
.
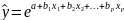Линеаризующее
преобразование:
.
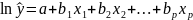3)
Обратная регрессионная модель:
.
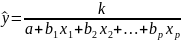Линеаризующее
преобразование:
.
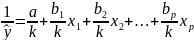К моделям, полученным после проведения линеаризующих преобразований можно применять обычные методы исследования линейной регрессии. Но поскольку в них присутствуют не фактические значения изучаемого показателя, то оценки параметров получаются несколько смещенными. При анализе линеаризуемых функций регрессии, следует особенно тщательно проверять выполнение предпосылок метода наименьших квадратов.
14. Коэффициент эластичности
Коэффициент эластичности показывает степень количественного изменения одного фактора (например, объема спроса или предложения) при изменении другого (цены, доходов или издержек) на1%.
Методы подсчета коэффициента эластичности
При подсчете коэффициента эластичности используют два основных метода:
Эластичность
по дуге (дуговая эластичность)
— применяется при измерении эластичности
между двумя точками на кривой спроса
или предложения и предполагает знание
первоначальных и последующих уровней
цен и объемов.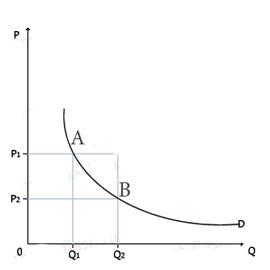
P1- начальная
ценаP2-
нов.ц. Q1-началь оюъем Q2- нов объем
Эластичность
в точке
(точечная эластичность) — используется
в том случае, когда задана функция
спроса (предложения) и исходный уровень
цены и величины спроса (или предложения).
Данная формула характеризует относительное
изменение объема спроса (или предложения)
при бесконечно малом изменении цены
(или какого-либо другого параметра).
, где
— производная функции спроса (или
предложения) по цене;
— рыночная цена;
— величина спроса (или предложения)
при данной цене.