11.Использование метода Фишера для оценки значимости регрессии. Коэффициент детерминации.

При анализе адекватности уравнения регрессии (модели) исследуемому процессу, возможны следующие варианты:

1. Построенная модель на основе F-критерия Фишера в целом адекватна и всекоэффициенты регрессии значимы. Такая модель может быть использована для принятия решений и осуществления прогнозов.

2. Модель по F-критерию Фишера адекватна, но часть коэффициентов  не значима. Модель пригодна для принятия некоторых решений, но не для прогнозов.

3. Модель по F-критерию адекватна, но все коэффициенты регрессии не значимы. Модель полностью считается неадекватной. На ее основе не принимаются решения и не осуществляются прогнозы.

Проверить значимость (качество) уравнения регрессии–значит установить, соответствует ли математическая модель, выражающая  зависимость между переменными, экспериментальным данным, достаточно ли включенных в уравнение  объясняющих  переменных для описания зависимой переменной. Чтобы иметь общее суждение о качестве модели, по каждому наблюдению из относительных отклонений определяют среднюю ошибку аппроксимации. Проверкаадекватности уравнения регрессии (модели) осуществляется с помощью средней ошибки аппроксимации, величина которой  не должна превышать 10-12% (рекомендовано).

Оценка значимости уравнения  регрессии в целом производится на основе F-критерия Фишера, которому предшествует дисперсионный анализ. В математической  статистике  дисперсионный  анализ  рассматривается  как самостоятельный  инструмент  статистического  анализа. В эконометрике он применяется как вспомогательное средство для изучения  качества регрессионной модели. Согласно основной идее дисперсионного анализа, общая сумма квадратов  отклонений  переменной (y) от среднего значения  (y_ср.)  раскладывается на две части – «объясненную»и «необъясненную»:

Схема дисперсионного анализа имеет следующий вид:

(n –число наблюдений,  m–число параметров при переменной  x)

Определение  дисперсии  на  одну  степень  свободы  приводит  дисперсии к  сравнимому  виду.  Сопоставляя  факторную  и  остаточную  дисперсии  в расчете на одну степень свободы, получим величину  F-критерия Фишера. Фактическое  значение  F -критерия  Фишера  сравнивается  с табличным значением F_табл. (α, k₁, k₂)  при заданном уровне значимости α и степенях свободы k₁= m и k₂=n-m-1.  При  этом,  если  фактическое  значение  F-критерия  больше  табличного F_факт > F_теор, то  признается статистическая  значимость уравнения в целом. Для парной линейной регрессии m=1 , поэтому:

12. Гетероскедастичность, способы обнаружения и исправления. Метод взвешенных наименьших квадратов.

Гетероскедастичность — понятие, используемое в эконометрике, означающее неоднородность наблюдений, выражающуюся в неодинаковой (непостоянной) дисперсии случайной ошибки регрессионной (эконометрической) модели. Гетероскедастичность противоположна понятию гомоскедастичность, которое означает однородность наблюдений, то есть постоянство дисперсии случайных ошибок модели.

Наличие гетероскедастичности случайных ошибок приводит к неэффективности оценок, полученных с помощью метода наименьших квадратов. Кроме того, в этом случае оказывается смещённой и несостоятельной классическая оценка ковариационной матрицы МНК(Метод наименьших квадратов)-оценок параметров. Следовательно статистические выводы о качестве полученных оценок могут быть неадекватными. В связи с этим тестирование моделей на гетероскедастичность является одной из необходимых процедур при построении регрессионных моделей.

Если дисперсия остатков изменяется для каждого наблюдения или группы наблюдений, т.е. , где, в общем случае, - неизвестный параметр, а S- известная симметричная положительно определенная матрица, то такое явление называется гетероскедастичностью. Если же , то имеем гомоскедастичность.

В случае простой однофакторной модели устранить гетероскедастичность просто. Достаточно левую и правую часть модели поделить на X. Для многофакторной модели такое преобразование значительно усложняется.

Для проверки наличия гетероскедастичности используют четыре метода, в зависимости от природы исходных данных: критерий , параметрический тест Гольдфельда-Квандта, непараметрический тест Гольдфельда-Квандта, тест Глейсера. Приведем алгоритмы каждого из методов.

Критерий применяется в случае значительной совокупности исходных данных.

Шаг 1. Значения показателя Y разбиваются на k групп в соответствии с изменениями уровня величины Y (по возрастанию, например).

Шаг 2. По каждой группе данных вычисляем сумму квадратов отклонений , .

Шаг 3. Определим сумму квадратов отклонений в целом по совокупности наблюдений:

, де - количество элементов в r- й группе.

Шаг 4. Вычислим параметр 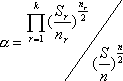, де n - количество наблюдений.

Шаг 5. Вычислим значение критерия , который приблизительно отвечает распределению со степенью свободы k-1, если дисперсия всех наблюдений однородна.

Таким образом, если значение не меньше табличного значения при выбранном уровне доверия и степени свободы k-1, то принимается гипотеза о наличии гетероскедастичности.

Параметрический тест Гольдфельда-Квандта применяется, если количество наблюдений невелико и сделано предположение о том, что дисперсия остатков возрастает пропорционально квадрату одной из независимых переменных, т.е. .

Шаг 1. Упорядочить наблюдения в соответствии с величиной элементов вектора Xk, для которого предположительно выполняется вышеприведенное равенство.

Шаг 2. Исходя из соотношения , предложенного авторами метода, где n - количество элементов Xk, выбросить c наблюдений, которые находятся в средине вектора.

Шаг 3. Согласно МНК построить две эконометрические модели по двум полученным совокупностям наблюдений размером n-c/2, естественно при условии, что n-c/2>m, где m - количество независимых факторов, присутствующих в модели.

Шаг 4. Найти сумму квадратов остатков для первой и второй моделей: и .

Шаг 5. Вычислить значение критерия , который соответствует F- критерию со степенями свободы.

Таким образом, если , то гипотеза об отсутствии гетероскедастичности принимается.

Метод наименьших квадратов (МНК) — один из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным. Метод основан на минимизации суммы квадратов остатков регрессии. Взвешенный МНК. В случае диагональной весовой матрицы (а значит и ковариационной матрицы случайных ошибок) имеем так называемый взвешенный МНК. В данном случае минимизируется взвешенная сумма квадратов остатков модели, то есть каждое наблюдение получает «вес», обратно пропорциональный дисперсии случайной ошибки в данном наблюдении: . Фактически данные преобразуются взвешиванием наблюдений (делением на величину, пропорциональную предполагаемому стандартному отклонению случайных ошибок), а к взвешенным данным применяется обычный МНК.