Метод искусственного базиса

Данный метод применяется, если система линейных ограничений содержит равенства, но не является системой из базиса.

Пример:

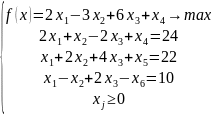
Вспомним условия применения симплекс-метода: правые части неотрицательны, присутствуют базисные переменные. Первое условие выполняется, а второе выполняется лишь частично: базисными переменными являются только и , а переменная базисной не является, т. к. входит в равенство со знаком минус.

Добавим искусственную базисную переменную :

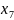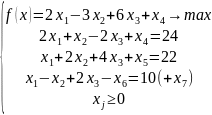
В связи с этим изменится целевая функция:

Т. е. искусственные базисные переменные у нас добавляются в целевую функцию с отрицательным знаком и при коэффициенте .

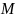Теперь можем строить нашу симплекс-таблицу. Отличием от обычной в ней будет наличие строки и столбца . Заполнение происходит точно так же, как и в обычном случае. В строку помещаются коэффициенты при , которые встречаются во всех скалярных произведениях.

Базисные перемен.			2	-3	6	1	0	0
	1 0	24 22 10	2 1 1	1 2 -1	-2 4 2	1 0 0	0 1 0	0 0 -1	0 0 1
		24	0	4	-8	0	0	0	0
		-10	-1	1	-2	0	0	1	0

Пересчёт ведём по строке до тех пор, пока не все искусственные переменные будут исключены из базиса. Если получившаяся таблица оптимальна, то пересчёт заканчивают. В противном случае продолжаем пересчёт симплекс-таблицы по строке . Все действия выполняются так же, как и в обычном случае.

Выберем ключевой элемент.

После первого зануления переменная входит в базис вместо . Поэтому в следующей симплекс-таблице столбца и строки не будет.

Базисные перемен.			2	-3	6	1	0	0
	1 0	24 22 10	2 1 1	1 2 -1	-2 4 2	1 0 0	0 1 0	0 0 -1	0 0 1
	24	0	4	-8	0	0	0	0	0
	-10	-1	1	2	0	0	1	1	0
	0 6	34 2 5	3 -1 1/2	0 4 -1/2	0 0 1	1 0 0	0 1 0	-1 2 1/2
		64	4	0	0	0	0	-4
	1 0 6	35 1 5 1/2	5/2 -1/2 1/4	2 2 1/2	0 0 1	1 0 0	1/2 1/2 1/4	0 1 0
		68	2	8	0	0	2	0

На этом этапе таблица оптимальна. Запишем полученный план: 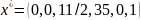. Значение целевой функции в этом плане: .

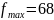Задача будет неразрешима, если в столбце последний элемент отрицательный, а все вышестоящие элементы неотрицательные.

Важным отличием данного метода является то, что базисные переменные являются искусственными – их добавление в левую часть уравнения не влияет на знак равенства.