
МЕТОДЫ ОПТИМИЗАЦИИ Горлова Светлана Николаевна |
06.09.2012 Лекция |
Курс: домашние работы, контрольная работа, зачёт.
§1. Общая поставнока задач
Линейного программирования.
Под программированием здесь подразумевается планирование.
Определение:
Задачей линейного программирования будем называть задачу отыскания наибольшего или наименьшего значения линейной функции на некотором множестве.
Задача имеет следующий внешний вид:
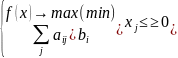
Это система линейного ограничения.
где:
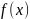 – целевая функция или критерий
оптимальности
– целевая функция или критерий
оптимальности
 – любой знак
– любой знак
Целевая функция чаще всего имеет вид:
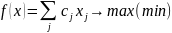
Определение:
Задача линейного программирования называется стандартной, если:
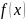 на
на
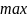
 для любых
для любых

Ограничения имеют вид неравенств
 (СЭЛП)
(СЭЛП)
Определение:
Задача линейного программирования называется канонической, если выполняются первой и второе из перечисленных выше условий, а ограничения имеют вид равенств.
Определение:
Множество
 называется множеством планов или
допустимых решений. Иными словами, если
называется множеством планов или
допустимых решений. Иными словами, если
 ’ы
удовлетворяют решениям задачи, то
множество
будет планом допустимых решений задачи.
’ы
удовлетворяют решениям задачи, то
множество
будет планом допустимых решений задачи.
Определение:
План
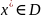 называется оптимальным в задаче на
,
(или на
называется оптимальным в задаче на
,
(или на
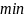 )
если
)
если
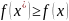 (или
(или
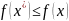 )
для любых
)
для любых
 .
.
Рассмотрим несколько задач линейного программирования.
Задача о пищевом рационе.
Имеется
три вида продуктов:
 ,
,
 ,
,
 .
Из этих продуктов требуется составить
пищевой рацион, который должен содержать:
.
Из этих продуктов требуется составить
пищевой рацион, который должен содержать:
белков
не менее
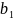 ед.
ед.
углеводов
– не менее
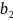 ед.
ед.
жиров
– не менее
 ед.
ед.
Содержание белков, углеводов и жиров в одной единице продукции каждого вида указано в таблице:
-
Вид продукции
белки
жиры
углеводы
Стоимость единицы продукции

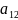


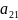
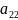

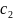
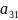
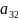
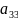

Составить пищевой рацион таким образом, чтобы выполнялись условия по белкам, углеводам и жирам, и стоимость рациона была минимальной.
Cоставим задачу.
 – это количество единиц той или иной
продукции.
– это количество единиц той или иной
продукции.
Составим ограничения.
Белков
в продукции
 будет
будет
 ,
т. к.
,
т. к.
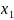 – это количество продукции
,
а
– это количество белков в одной единице
продукции. Тогда:
– это количество продукции
,
а
– это количество белков в одной единице
продукции. Тогда:

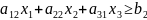
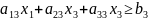
Определим целевую функцию. По условию задачи она стремится к минимуму:

И положим следующее ограничение: количество товаров не может быть отрицательным, т. е. .
Таким образом, задача имеет следующий вид:
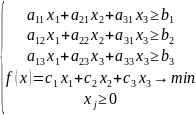
Задача о загрузке оборудования.
Предприятие
располагает двумя видами станков:
 штук первого вида,
штук первого вида,
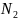 штук – второго вида. Станки могут
производить три вида ткани, но с различной
производительностью, которая указана
в таблице:
штук – второго вида. Станки могут
производить три вида ткани, но с различной
производительностью, которая указана
в таблице:
-
Вид станка
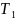
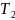
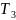
1
2
Доход от реализации ткани
Производительность и стоимость указаны на одну единицу ткани.
План:
не менее
,
но не более

не менее
,
но не более

не менее
,
но не более
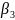
Требуется распределить загрузку станков производством ткани так, чтобы доход от реализации был бы максимальным, и все без исключения станки работали.
В
качестве переменных
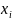 попробуем для начала взять количество
единиц ткани.
попробуем для начала взять количество
единиц ткани.
Необходимо
произвести
,
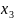 ,
единиц ткани типа
,
,
так, чтобы максимизировать выручку.
Получаем функцию:
,
единиц ткани типа
,
,
так, чтобы максимизировать выручку.
Получаем функцию:
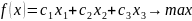
Ограничения по выпуску тканей определённого типа:
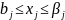 ,
,
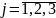
Но
теперь не ясно, как определить загрузку
станков, ведь они оба должны работать
одновременно. Получается, что в качестве
переменных
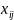 у нас будет количество станков -го вида,
занятых производством ткани
-го
типа.
у нас будет количество станков -го вида,
занятых производством ткани
-го
типа.
Теперь узнаем, сколько ткани разного типа вида мы выпустим. Здесь пригодится информация о производительности станков.
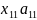 – это количество ткани 1-го типа,
выпущенной 1-м станком,
– это количество ткани 1-го типа,
выпущенной 1-м станком,
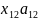 – это количество ткани 2-го типа,
выпущенной 1-м станком,
– это количество ткани 2-го типа,
выпущенной 1-м станком,
 – это количество ткани 3-го типа,
выпущенной 1-м станком,
– это количество ткани 3-го типа,
выпущенной 1-м станком,
 – это количество ткани 1-го типа,
выпущенной 2-м станком,
– это количество ткани 1-го типа,
выпущенной 2-м станком,
 – это количество ткани 2-го типа,
выпущенной 2-м станком,
– это количество ткани 2-го типа,
выпущенной 2-м станком,
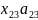 – это количество ткани 3-го типа,
выпущенной 2-м станком.
– это количество ткани 3-го типа,
выпущенной 2-м станком.
Тогда ограничения по количеству выпущенной ткани будут выглядеть так:
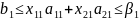

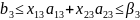
Целевая функция получается следующая:
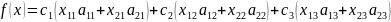
Одновременность работы станков последует из следующих ограничений:
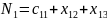

Количество работающих станков не может быть нулевым и должно быть целым, т. е.:
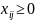

Таким образом, мы составили задачу.
ГЕОМЕТРИЧСЕКАЯ ИНТЕРПРЕТАЦИЯ
ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ.
Задание: решить геометрически.

Построим
область на координатной плоскости,
зная, что
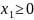 ,
,
 .
Для этого найдём точки, через которые
проходит каждая из пяти прямых.
.
Для этого найдём точки, через которые
проходит каждая из пяти прямых.
Первая
прямая
 ,
очевидно, проходит через точки
,
очевидно, проходит через точки
 и
и
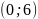 :
:
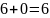 ,
,
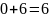 .
.
Вторая
прямая
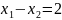 проходит через точки
проходит через точки
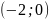 и
и
 .
.
Остальные прямые совпадают с координатными осями.
Построим
ограниченную данными прямыми область
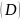 :
:
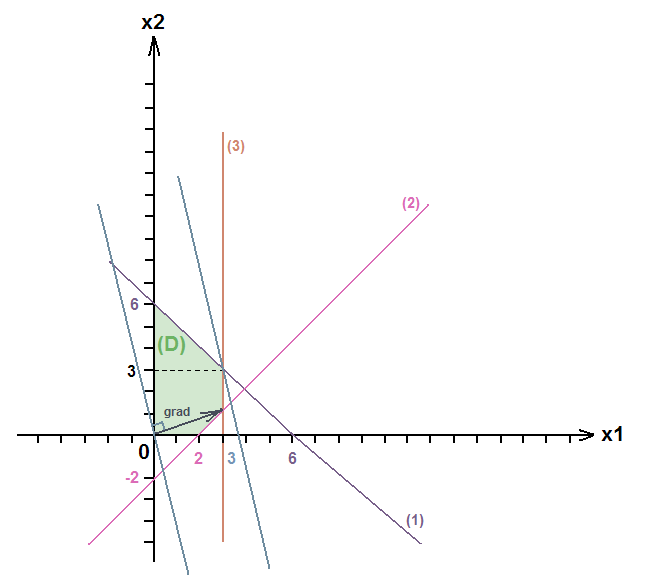
По
условию нужно найти наибольшее значение
функции на данной области (значение
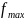 ).
Функция принимает наибольшее значение
в одной из точек пересечения целевой
функции
и найденной области
.
Чтобы найти эту точку, нам необходимо
установить направление наискорейшего
возрастания функции. Оно определяется
вектором-градиентом:
).
Функция принимает наибольшее значение
в одной из точек пересечения целевой
функции
и найденной области
.
Чтобы найти эту точку, нам необходимо
установить направление наискорейшего
возрастания функции. Оно определяется
вектором-градиентом:
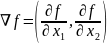
По
условию целевая функция имеет вид
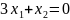 .
Найдём её первые частные производные:
.
Найдём её первые частные производные:


Таким
образом, вектор-градиент направлен из
начала координат в точку
 .
.
Проведём
перпендикуляр к градиенту и выполним
его параллельный перенос в ту сторону,
в которую направлен наш градиент.
Переносим до тех пор, пока не встретим
самую последнюю в этом направлении
точку области
.
В этой точке функция будет принимать
наибольшее значение. Как видно по
графику, это точка пересечения прямых
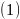 и
и
 с координатами
с координатами
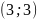 .
.
Подставим найденную точку в уравнение целевой функции, чтобы найти максимальное значение функции в данной области:
 .
.
13.09.2012 Лекция |
Запишем задачу линейного программирования в векторной форме. Вспомним вид обычной записи задачи линейного программирования:
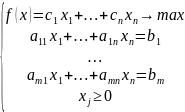
Видим,
что правая часть целевой функции
напоминает скалярное произведение
векторов. Таким образом, целевая функция
представима в виде скалярного произведения
векторов
 и
:
и
:

Ограничения же – это уравнения, которые в векторной форме можно представить так:

где
 для любых
для любых


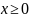
План
из
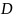 называется опорным, базисным, если он
либо нулевой вектор, либо если система
вектор-столбцов, соответствующих
ненулевым координатам вектора х, является
линейно независимой.
называется опорным, базисным, если он
либо нулевой вектор, либо если система
вектор-столбцов, соответствующих
ненулевым координатам вектора х, является
линейно независимой.
Пример:
Является ли вектор базисным (опорным)?
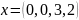

Но прежде чем проверять опорность плана , следует сначала удостовериться, что является планом, т. е. принадлежит множеству . Для этого подставим вектор в ограничения:
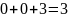
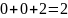
Следовательно, вектор принадлежит множеству , т. е. является планом.
Теперь проверим, является ли план базисным, для этого воспользуемся определением. Т. к. вектор не является нулевым, построим систему вектор-столбцов:
Из вектора только третья и четвёртая координаты является ненулевыми.
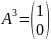

Установим
наличие или отсутствие линейной
зависимости этих двух векторов. Помним,
что система векторов
 является линейно зависимой, если
существуют такие
является линейно зависимой, если
существуют такие
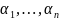 ,
не все равные нулю, при которых
,
не все равные нулю, при которых
 .
.
Следовательно, система векторов не является линейно зависимой. Таким образом, можем сделать заключение: план является базисным (опорным).
Определение:
Точка
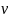 множетсва
множетсва
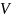 называется угловой точкой множества
,
если она не является внутренней точкой
никакого отрезка.
называется угловой точкой множества
,
если она не является внутренней точкой
никакого отрезка.
Определение:
Множество называется выпуклым, если оно вместе с любыми двумя точками содержит и весь отрезок, заключённый между этими точками.
Запишем условие принадлежности отрезка всему множеству:
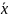 ,
,

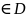
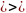
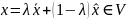 ,
,

Теорема:
Каждый базисный план является угловой точкой множества допустимых планов.
Доказательство:
Существует некий , являющийся планом, т. е. . Кроме того, по условию – базис. Докажем, что – угловая точка.
Поскольку
базисный, у него есть как нулевые, так
и ненулевые координаты. Допустим,
 .
Из этого следует, что система
.
Из этого следует, что система
 линейно независима.
линейно независима.
Докажем
от противного, т. е. пусть
не является угловой точкой, другими
словами,
– внутренняя точка некоторого отрезка.
Отсюда следует, что
 ,
где
,
.
Запишем это равенство в координатном
виде:
,
где
,
.
Запишем это равенство в координатном
виде:
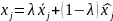 ,
,
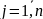 .
.
 ,
,
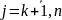
По
условию задачи линейного программирования,
координаты у допустимых планов
неотрицательны, т. е.
 и
и
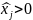 .
.
Т.
к.
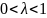 ,
то в правой части последнего равенства
стоит сумма неотрицательных слагаемых.
Это происходит тогда, когда все члены
равенства равны нулю, т. е.
,
то в правой части последнего равенства
стоит сумма неотрицательных слагаемых.
Это происходит тогда, когда все члены
равенства равны нулю, т. е.
 ,
.
Т. е. у векторов
и
нулю равны одни и те же координаты.
,
.
Т. е. у векторов
и
нулю равны одни и те же координаты.
Т.
к.
,
,
они удовлетвряют ограничениям задачи:
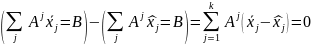 .
Для
.
Для
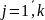
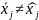 .
Т. е. система вектор-столбцов
– линейно зависима <дописать здесь>.
.
Т. е. система вектор-столбцов
– линейно зависима <дописать здесь>.
Теорема:
Если целевая функция принимает наибольшее значение в некоторой точке множества D, то она принимает это же значение и в некоторой угловой точке этого множества.
Доказательство:
Воспользуемся
известным фактом: если D
замкнутое, имеющее конечное число
угловых точек (скажем, D
– это какой-либо многоугольник), то
любую точку из D можно
представить в виде линейной комбинации
угловых точек, т. е. если векторы
 – угловые точки множества D,
то для любых
верно следующее:
– угловые точки множества D,
то для любых
верно следующее:

где
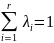
Т. е. любая точка множества представима в виде угловой точки.
Пусть
для любых
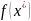 принимает наибольшее значение в точке
принимает наибольшее значение в точке
 (скалярное произведение линейно по
каждому сомножителю)
(скалярное произведение линейно по
каждому сомножителю)
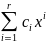 .
.
Выберем среди угловых точек такую, в которой целевая функция принимает наибольшее значение. Такую точку выбрать возможно, ведь у нас конечное множество угловых точек. Среди угловых точек выберем такую, значение которой в целевой функции является наибольшим.
<дописать здесь>
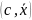 .
.
Итак,
 .
.
Но
с другой стороны,
:
 – наибольшее, т. е. для любого
из
– наибольшее, т. е. для любого
из
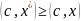 следует
следует
 .
.
Из
этого следует, что
 .
Что и требовалось доказать.
.
Что и требовалось доказать.
Задача 1.
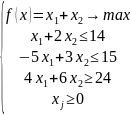
Решить нужно графически.
Построим область, ограниченную нашими прямыми и осями координат:
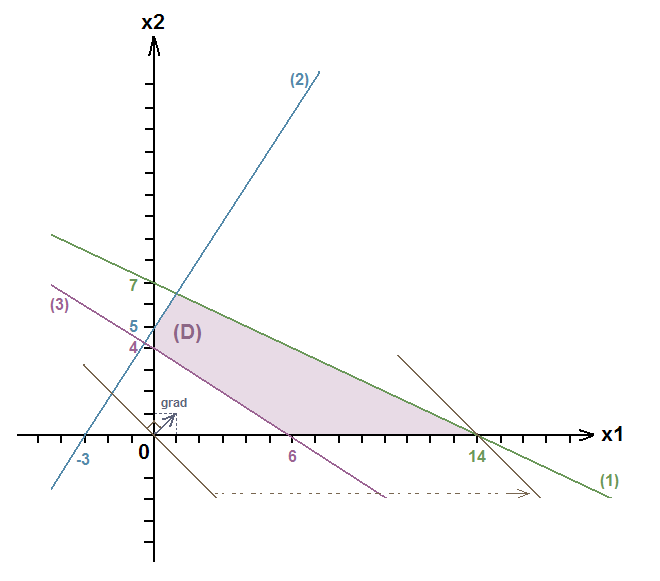
Найдём координаты вектора-градиента:
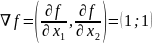
Прямую,
перпендикулярную вектору-градиенту,
параллельно переносим до пересечения
с самой последней точкой, у нас это точка
пересечения прямой
 с осью координат
с осью координат
 .
Составим и решим систему:
.
Составим и решим систему:
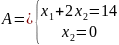
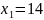 ,
,
 – это и есть точка, в которой целевая
функция принимает наибольшее значение.
– это и есть точка, в которой целевая
функция принимает наибольшее значение.
Найдём значение целевой функции в этой точке:

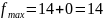 .
.
Задача 2.
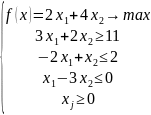
Построим область
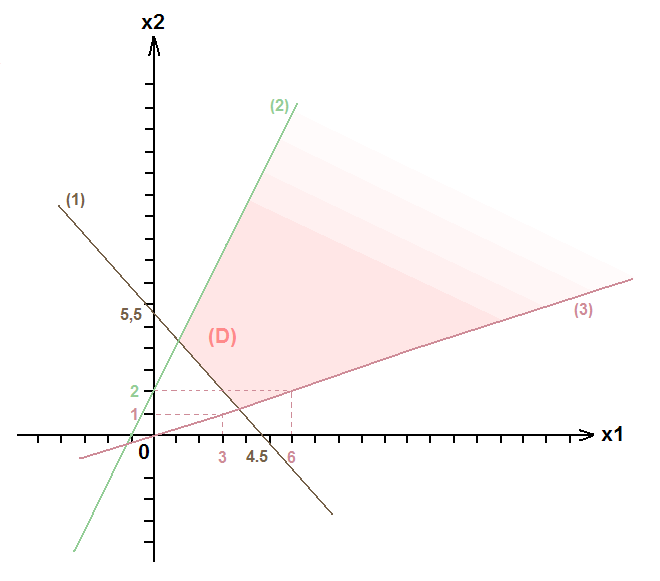
Как видно на графике, область не ограничена. Следовательно, наибольшего значения у функции нет, задача решения не имеет. Целевая функция не ограничена сверху на непустом множестве планов.
14.09.2012 Лекция |
Задача 3.
Продолжаем решать графически:

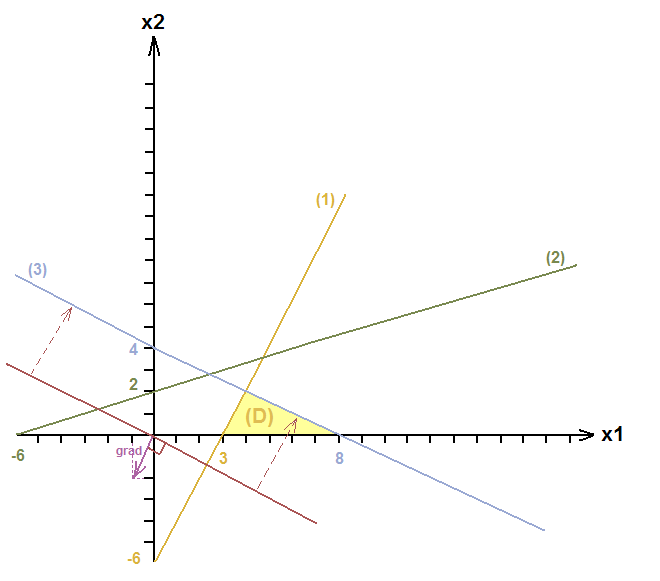
Вектор-градиент
откладывается из начала координат в
точку, координаты которой составлены
из коэффициентов при целевой функции.
Например, координатами вектора-градиента
в этой задаче будут ( ),
а направлен вектор-градиент всегда из
начала координат.
),
а направлен вектор-градиент всегда из
начала координат.
Как
мы помним, градиент показывает направление
возрастания функции. Поэтому в задачах
со стремящейся к минимуму целевой
функцией мы переносим перпендикуляр
градиента в ту сторону, которая
противоположна его направлению. В этой
задаче перпендикуляр градиента параллелен
3-ей прямой, а значит, при параллельном
переносе он полностью накладывается
на эту прямую. Это можно увидеть также
по коэффициентам при аргументах целевой
функции и третьего уравнения – они
пропорциональны. Ответом к задаче будет
множество точек, расположенных на том
отрезке прямой
,
который сходит в область
.
Другими словами, это будут точки,
расположенные на отрезке
 с координатами концов (
с координатами концов (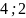 )
и (
)
и ( ).
).
Наш
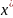 будет записан в виде:
будет записан в виде:
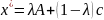 .
.
Подставим
координаты концов отрезка
 и
и
 в целевую функцию:
в целевую функцию:

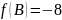
Таким
образом, наименьшее значение целевой
функции:
 .
.
Задача 4.
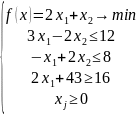
<При желании решить эту задачу дома>
Задача 5.

Замечаем,
что у нас больше двух переменных. Нам
нужно выразить их все через
и
 .
Тогда целевая функция примет вот такой
вид:
.
Тогда целевая функция примет вот такой
вид:
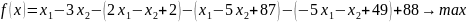
Упростим:

Теперь замечаем, что у нас нет неравенств. Без неравенств нам не удастся построить область. Чтобы получить неравенство из равенства, нужно одну из его частей увеличить или уменьшить. Видим, что наши – неотрицательные, поэтому достаточно будет убрать из первой части уравнения любой , чтобы точно получилось неравенство.
Уберём из левой части весь последний столбец ’ов:
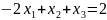
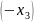
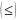

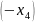

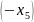
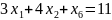




Таким образом, мы не только создали неравенства, но и избавились от столбца лишних переменных, и теперь сможем построить область.
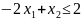

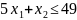


Находим:

19.09.2012 Лекция |
