9.RISC-идеология. История, основные принципы, тенденция развития, "пострисковые" архитектуры: концепции VLIW и EPIC.
10.Понятие конвейера. "Жадная" стратегия. Понятие MAL в теории конвейера.
3. Раздел "Схемотехника ЭВМ"
Литература:
1. 681.3 С92 Схемотехника ЭВМ: Учебник для студентов вузов спец. ЭВМ/ Под редакцией Г.Н. Соловьёва. М.: Высшая школа, 1985395 с.
2*. 681.3 К17 Кларин Б.И., Ковригин Б.Н., Тышкевич В.Г. Схемотехника ЭВМ. Лабораторный практикум / Под редакцией Б.И. Кальнина. 2-е издание, переработанное и дополненное. Учебное пособие. М.: МИФИ, 1999. - 172 с.
3*. 681.3 А76 Ковригин Б.Н., Сидуков В.М., Мифтахов Р.К. и др. / Под редакцией Б.Н. Ковригина: Учебное пособие. М.: 1991. - 84 с.
4. Угрюмов Е.П. Цифровая схемотехника. - СПб, 2000, 528 с.
*) см. в интернете на сайте кафедры http://dozen.mthpi в разделе "СтудентуРекомендуемая литература - 3-й курс" - Схемотехника ЭВМ.
1. Этапы проектирования комбинационных схем на примере дешифратора на 4 выхода: определение, таблица истинности, функция, логическая схема. Увеличение разрядности до 16-ти выходов.
ЗАДАЧА: реализовать функцию F1(X2,X1,X0)=Σ(0,1,4,6,7) на дешифраторе.
Этапы проектирования комбинационных схем (?):
1. Составляем таблицу истинности
2. Проводим минимизацию и записываем функцию
3. Переводим функцию в нужный базис и строим схему 4. По схеме стоим временную диаграмму и определяем временные параметры схемы.
Дешифратор Определение: Дешифратор (DC) - комбинационная схема. Она будет иметь n входов и 2n выходов (полный дешифратор). При любой комбинации
поступающих на вход сигналов всегда будет возбуждён только один из выходов. Номер этого возбуждённого выхода будет определяться номером набора.
Таблица истинности (на примере дешифратора на 4 выхода):
E |
Номер набора |
X2 |
X1 |
|
F0 |
F1 |
F2 |
F3 |
0 |
|
X |
X |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
2 |
1 |
0 |
|
0 |
0 |
1 |
0 |
1 |
3 |
1 |
1 |
|
0 |
0 |
0 |
1 |
Функция (списываем с таблицы истинности):
F0 = X 2 X1 , F1 = X 2 X1 , F 2 = X 2 X1, F3 = X 2 X1
Логическая схема: схема реализации полного дешифратора 2 → 4 (дешифратор на 4 выхода)
Увеличение разрядности до 16-ти Рассмотрим построение полного дешифратора на 16 выходов из дешифраторов 2 → 4 .
При этом для 16-ти выходов число входов будетn=4 (т.к. 16 = 2n ).
Для увеличения разрядности дешифратора можно применить каскадную схему из дешифраторов (аналогично схеме на мультиплексорах). При этом на входы E (Enable - разрешение) подаются выходы первого дешифратора.
Поскольку на выходе мы должны получить толькоодну единицу, представленную схему можно рассмотреть как коммутацию входной единицы, которая поступает на вход E первого дешифратора. В зависимости от значений адресных входов X1-X2 (старшие разряды), 1 поступает на один из 4-х дешифраторов (на такой же E-вход). Далее, в зависимости от значений младших разрядов (X1-X0) поступившая "1" коммутируется на один из выходов.
Реализация заданной функции на дешифраторе (ЗАДАЧА):
ЗАДАЧА: реализовать функцию F1(X2,X1,X0)=Σ(0,1,4,6,7) на дешифраторе.
Для реализации логической функции на дешифраторе необходимо завести соответствующие выходы дешифратора (на которых функция принимает единичное значение) на элемент "ИЛИ", если выходы прямые или на элемент " И-НЕ", если выходы инверсные.
2. Этапы проектирования комбинационных схем на примере мультиплексора 4-1: определение, таблица истинности, функция, логическая схема. Увеличение разрядности до 16-1.
ЗАДАЧА: реализовать функцию F2(X3,X2,X1,X0)=Σ(0,2,6,7,8,9,13,14) на мультиплексоре.
3. Этапы проектирования комбинационных схем на примере схем сравнения двухразрядных слов: определение, таблица истинности, функция, логическая схема. Схема сравнения четырёхразрядных слов на элементах "Исключающее ИЛИ".
Этапы проектирования комбинационных схем (см. билет 1).
Функция "исключающее ИЛИ". Выполняет функцию - сумма по модулю два (он же называется ещё и "управляемым инвертером"). Ноль на выходе будет только в случае равенства двух операндов.
Управляемая инверсия: если считать, что а - это управляющий вход (см. схему), то получается, что при 0 передаём b напрямую, при 1 - инвертируем.
Сравнение двухразрядных слов (на исключающих ИЛИ):
Определение: Схема сравнения - это логическая комбинационная схема, на выходе которой ноль будет только в случае равенства операндов.
Таблица истинности (0 будет там, где значения операндов A и B равны):
Первый операнд |
Второй операнд |
Сравнение |
||
A1 |
A0 |
B1 |
B0 |
F |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
Во всех остальных случаях |
1 |
|||
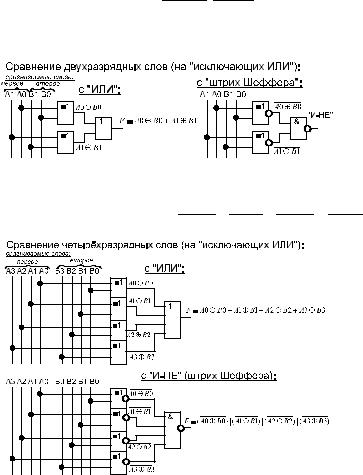
То есть - сначала поразрядно сравниваются операнды, и если хотя бы один из разрядов не совпадает (результат сравнения =1), то и числа в целом не равны (эта единица должна пойти на выход). То есть - сначала должны быть элементы "Исключающее ИЛИ", а далее элемент "ИЛИ" (где - если хотя бы одна единица на входе, то на выходе будет 1).
Получаем следующую функцию:
F = A0 B0 + A1 B1 или: F = (A0 B0) | (A1 B1)
где A0 - младшие разряды первого операнда, A1 - старшие (аналогично для второго операнда B).
Логическая схема (по функции):
Схема сравнения четырёхразрядных слов (на исключающих ИЛИ):
Функция (по аналогии с двумя операндами): F = A0 B0 + A1 B1+ A2 B2 + A3 B3 . Или, для реализации на ТТЛ-микросхем: F = (A0 B0) | (A1 B1) | (A2 B2) | (A3 B3)
4.Сумматор: определение, таблица истинности одноразрядного сумматора, функции суммы и переноса, логическая схема, временные параметры. Схема 4-х разрядного сумматора с последовательным переносом, время суммирования.
5.Синтез одновыходных комбинационных схем. Этапы проектирования на базисе И-НЕ.
Задача: выполнить синтез комбинационной схемы для функции F4(X3,X2,X1,X0)= Σ(0,1,6,7,8,9,10,11). Построить временную диаграмму, записать выражения для максимальных задержек переключения выходного сигнала.
Этапы проектирования комбинационных схем (?):
1.Составляем таблицу истинности
2.Проводим минимизацию и записываем функцию
3.Переводим функцию в нужный базис и строим схему
4.По схеме стоим временную диаграмму и определяем временные параметры схемы(в
данном случае - максимальную задержку переключения выходного сигнала).
1. Таблица истинности: (в условии задачи указаны номера наборов, на которых функция принимает единичное значение):
№ набора |
X3 |
|
X2 |
|
X1 |
|
X0 |
|
Значение функции |
0 |
0 |
|
0 |
|
0 |
|
0 |
|
1 |
1 |
0 |
|
0 |
|
0 |
|
1 |
|
1 |
2 |
0 |
|
0 |
|
1 |
|
0 |
|
0 |
3 |
0 |
0 |
1 |
1 |
|
0 |
|||
4 |
0 |
1 |
0 |
0 |
|
0 |
|||
5 |
0 |
1 |
0 |
1 |
|
0 |
|||
6 |
0 |
|
1 |
|
1 |
|
0 |
|
1 |
7 |
0 |
|
1 |
|
1 |
|
1 |
|
1 |
8 |
1 |
|
0 |
|
0 |
|
0 |
|
1 |
9 |
1 |
|
0 |
|
0 |
|
1 |
|
1 |
10 |
1 |
|
0 |
|
1 |
|
0 |
|
1 |
11 |
1 |
|
0 |
|
1 |
|
1 |
|
1 |
12 |
1 |
|
1 |
|
0 |
|
0 |
|
0 |
13 |
1 |
1 |
0 |
1 |
|
0 |
|||
14 |
1 |
1 |
1 |
0 |
|
0 |
|||
15 |
1 |
1 |
1 |
1 |
|
0 |
|||
2. Минимизация. Методом диаграмм Вейча:
3. Переводим функцию в нужный базис и строим схему:
Полученную функцию переведём в базис "И-НЕ" (штрих Шеффера):
F = |
|
3 |
X 2 |
X1 |
+ X 3 |
|
2 |
+ |
|
2 |
|
1 |
=> F = ( |
|
3 | X 2 | X1) | (X 3 | |
|
2) | ( |
X |
2 | |
X |
1) |
|||
X |
X |
X |
X |
X |
X |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
ÍÅ |
|
|
ÍÅ |
ÍÅ ÍÅ |
|
ÍÅ |
ÍÅ |
ÍÅ |
ÍÅ |
|
||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
3−È |
|
2−È |
|
|
2−È |
|
|
3È −ÍÅ |
2È −ÍÅ |
2È |
−ÍÅ |
||||||||||
|
|
|||||||||||||||||||||||
|
|
|
|
|
3−ÈËÈ |
|
|
|
|
|
|
|
|
3È −ÍÅ |
|
|
|
|
|
|
||||
Строим схему:
4. По схеме стоим временную диаграмму и определяем максимальную задержку переключения выходного сигнала. Временные параметры элементов (масштаб для построения диаграммы: 1 клеточка = 30 нс):
Элементы |
|
0 →1 |
|
1 → 0 |
|
|
Логические элементы |
|
&, 1, | |
22 нс |
|
15 нс |
|
|
|
И-ИЛИ |
15 нс |
|
15 нс |
|
По временной диаграмме |
(см. рис |
) видно, что максимальная задержка переключений из 0 |
||||
в 1 представляет собой 3 переключения: |
0 →1 , 1 → 0 и 0 →1 . Максимальная задержка |
|||||
переключений из 1 в 0 |
- два переключения: 0 →1 и 1 → 0 . Запишем выражение для |
|||||
максимальной задержки (при реализации "НЕ" на элементах "И-НЕ"): t10Ç.MAX =tÇ01 + t10Ç = 22íñ +15íñ =37íñ