
- •А. Аппаратное обеспечение компьютеров
- •1. Раздел "Основы теории компьютеров"
- •2. Минимизация булевых функций с помощью диаграмм Вейча.
- •3. Определение и применение базиса при построении произвольных функций алгебры-логики.
- •4. Сложение и вычитание чисел с фиксированной запятой.
- •5. Умножение чисел с плавающей запятой.
- •6. Форматы команд.
- •7. Схема выполнения машинной двухадресной команды типа "Регистр-память" на однопроцессорном компьютере.
- •8. Схема выполнения машинной двухадресной команды типа "Регистр-регистр" на однопроцессорном компьютере.
- •2. Раздел "Архитектура вычислительных систем"
- •1. Архитектура кэш-памяти. Ассоциативное распределение информации в кэш-памяти.
- •2. Архитектура кэш-памяти. Прямое распределение (отображение) информации в кэш-памяти.
- •3. Архитектура векторного блока супер-ЭВМ CYBER-205. Особенности её конвейеров, обеспечивающие механизм "зацепления команд".
- •4. Векторные процессоры: структура аппаратных средств.
- •5. Пять основных архитектур высокопроизводительных ВС, их краткая характеристика, примеры.
- •6. SMP архитектура. Достоинства и недостатки. Область применения, примеры ВС на SMP.
- •7. MPP архитектура. История развития. Основные принципы. Концепция, архитектура и характеристики суперкомпьютера Intel Paragon.
- •8. Кластерная архитектура. Проблема масштабируемости. Примеры.
- •10. Понятие конвейера. "Жадная" стратегия. Понятие MAL в теории конвейера.
- •3. Раздел "Схемотехника ЭВМ"
- •1. Этапы проектирования комбинационных схем на примере дешифратора на 4 выхода: определение, таблица истинности, функция, логическая схема. Увеличение разрядности до 16-ти выходов.
- •2. Этапы проектирования комбинационных схем на примере мультиплексора 4-1: определение, таблица истинности, функция, логическая схема. Увеличение разрядности до 16-1.
- •3. Этапы проектирования комбинационных схем на примере схем сравнения двухразрядных слов: определение, таблица истинности, функция, логическая схема. Схема сравнения четырёхразрядных слов на элементах "Исключающее ИЛИ".
- •6. Синтез многовыходных комбинационных схем. Этапы проектирования в базисе И-НЕ.
- •7. Триггерные схемы: определение, классификация, условные графические обозначения, динамические параметры. Обобщённая структура двухступенчатого триггера, диаграмма его работы, условное графическое обозначение, динамические параметры.
- •8. Синтез двухступенчатого триггера по заданной таблице внешних переходов: таблица истинности, минимизация, схема. Построить временную диаграмму для двух переключений триггера, определить максимальные задержки переключений.
- •9. Счётчики: определение, модуль счётчика, динамические параметры. Примеры суммирующего, вычитающего и реверсивного счётчиков: схемы, временные диаграммы.
- •10. Счётчики: определение, модуль счётчика. Организация цепей переноса: схемы, динамические параметры. (CP)
- •11. Синтез синхронных счётчиков с заданным модулем на заданном типе триггера (DV, JK).
- •Б. Программное обеспечение компьютеров
- •4. Раздел "Алгоритмы и структура данных"
- •1. Понятие логических структур данных. Отображение структуры данных в памяти вектором и списком. Типы списков. Определение, основные операции; особенности их реализации.
- •2. Стек и очередь: определение, основные операции. Особенности выполнений операций при реализации стека и очереди вектором.
- •3. Стек и очередь: определение, основные операции. Особенности выполнения операций при реализации стека и очереди списком.
- •4. Просматриваемая динамическая таблица-вектор: определение, основные операции, особенности их реализации.
- •5. Просматриваемая динамическая таблица-список: определение, основные операции, особенности их реализации.
- •6. Упорядоченная таблица-вектор: определение, основные операции, особенности их реализации.
- •7. Таблица произвольного доступа: определение, основные операции, отображение в памяти. Функция рандомизации, её назначение.
- •9. Перемешанная таблица, использующая перемешивание сложением: определение, основные операции, особенности их реализации.
- •10. Перемешанная таблица, использующая перемешивание сцеплением: определение, основные операции, особенности их реализации.
- •5. Раздел "Базы данных"
- •1. Системы с базами данных. Понятие системы управления базами данных СУБД. Функции СУБД.
- •2. Понятие независимости от данных. Трёхуровневая архитектура ANSI-SPARC. Сравнительная характеристика уровней.
- •3. Модель данных. Назначение моделей данных. Компоненты моделей данных. Классификация моделей данных.
- •5. База данных реляционного типа. Основные понятия и структура реляционной модели. Реляционные языки. Основные правила целостности реляционной модели.
- •6. Реляционная алгебра. Основные операции реляционной алгебры.
- •7. Язык SQL. Операторы определения и манипулирования данными. Выборка данных из таблиц.
- •8. Модель данных "сущность-связь". Основные концепции и способы их представления на диаграммах. Современные методологии построения моделей "сущность-связь".
- •9. Нормализация отношений. Цель нормализации. Приведение к нормальным формам.
- •10. Жизненный цикл приложения баз данных. Основные фазы проектирования базы данных.
- •6. Раздел "Операционные системы"
- •1. Файловые системы современных операционных систем. Интерфейс пользователя для работы с файловой системой.
- •2. Принцип защиты данных в операционных системах. Управление правами доступа к файлам.
- •3. Способы группирования команд в операционных системах. Командные файлы. Программные каналы, конвейеры команд.
- •4. Обзор возможностей командных процессоров (оболочек) операционных систем.
- •5. Принципы организации многозадачного режима в операционных системах.
- •6. Коммуникационные средства многопользовательских операционных систем.
- •7. Генерация, конфигурирование, настройка операционной системы на потребности конкретного пользователя.
- •8. Средства и способы обеспечения многопользовательского режима в операционных системах.
- •9. Понятие процесса. Управление процессами в операционной системе UNIX.
- •10. Понятие программного канала. Средства управления программными каналами.
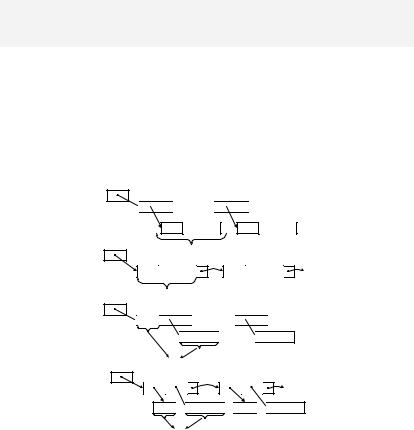
if(n == M) |
/* в конце таблицы нет свободной позиции */ |
if(garbage() < 0) /* "сборка мусора" */ |
|
return -2; |
/* в таблице нет свободной позиции */ |
/* включение нового элемента в таблицу |
*/ |
table[n].busy = 1; table[n].key = k; table[n++].info = dupl(in); return 0;
}
5. Просматриваемая динамическая таблица-список: определение, основные операции, особенности их реализации.
(Определение таблиц и просматриваемые таблицы - см. билет 4) (Алгоритмы и структуры данных, лекция 17.03.2004, 31.03.2004)
Просматриваемая динамическая таблица-список:
Варианты реализации (способы представления информации в зависимости от размещения таблицы в элементе списка):
1.Если динамическая просматриваемая таблица состоит из одинаковых элементов, элемент списка: ключ + информация + указатель на следующий элемент
2.Если элементы таблицы разного размеры, в элементе списка хранится только ссылка на информацию; однако это самый плохой по времени вариант.
3.Элемент таблицы делится на две части (ключ + информацию). Элемент списка содержит: ключ + ссылку на информацию + ссылку на следующий элемент списка.
head
a)
head
b)
head
c)










 ...
...
ключ информация |
ключ информация |
элемент таблицы |
|
ключ информация |
ключ информация |
...
элемент таблицы
 ключ
ключ 




 ключ
ключ 




 ...
...
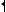 информация
информация
 информация
информация
элемент таблицы
head |
... |
ключ 
 информация
информация
 ключ
ключ 
 информация
информация
d)элемент таблицы
Вреальной ситуации в зависимости от конкретного типа таблиц можно использовать и более сложный способ отображения.
Пример: struct Item{
int key; Type info; Item *next;
};
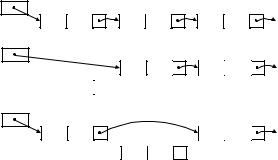
Item *ptab; |
/* указатель на начало таблицы */ |
Операции работы с таблицами:
1.Поиск (осуществляется простым просмотром списка)
2.Для динамических таблиц:
2.1.включить (вставить) в таблицу. Перед вставкой элемента - поиск по ключу (чтобы ключ вставляемого элемента остался уникальным для таблицы). Элемент вставляется в начало (!) списка (т.к. положение включаемого элемента роли не играет - целесообразно включать элемент в начало списка, используя соответствующий алгоритм стека).
2.2.удалить элемент из таблицы (при этом могут возникнуть некоторые затруднения - см. ниже).
При отображении просматриваемой таблицы-списка не играет роли, статическая она или динамическая (структура элемента таблицы будет одинакова).
Особенности операции удаления:
Проблема различных типов данных (чтобы не потерять указатель на начало) - для элементов, занимающих разное положение в списке, приходится выполнять разный набор операций. при удалении первого элемента должен изменяться указатель на начало таблицы, а при удалении промежуточного - поле указателя в предшествующем элементе списка.
Исходное состояние списка
k1 |
in1 |
k2 |
in2 |
k3 |
in3 |
... |
a) Удален первый элемент |
|
|
|
|
|
|
k2 |
in2 |
k3 |
in3 |
... |
k1 |
in1 |
|
b) Удален промежуточный элемент
k1 |
in1 |
k3 |
in3 |
... |
k2 in2
При удалении элемента надо:
1.Иметь доступ к предшествующему элементу списка. Решение: либо проверять положение удаляемого элемента, либо использовать двойной указатель.
2.Различать вид предшествующего элемента. Решение: поскольку операция поиска возвращает искомый элемент и не сообщает о месте его размещения в списке, при реализации операции удаления элемента из списка приходится либо:
2.1.повторять поиск элемента,
2.2.либо следует несколько изменить реализацию операции поиска.
При реализации с использованием двойных указателей:
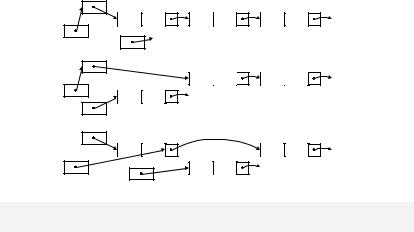
Исходное состояние списка |
|
|
|
|
|
||
ptab |
|
|
|
|
|
|
|
pptr |
k1 |
in1 |
k2 |
in2 |
k3 |
in3 |
... |
|
|
|
|
|
|
|
|
|
cur |
|
|
|
|
|
|
ptab a) Удаляется первый элемент |
|
|
|
|
|
||
pptr |
|
|
k2 |
in2 |
k3 |
in3 |
... |
k1 |
in1 |
|
|
|
|
|
|
cur |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
ptab b) Удаляется промежуточный элемент |
|
|
|
|
|||
|
k1 |
in1 |
|
|
k3 |
in3 |
... |
pptr |
cur |
|
k2 |
in2 |
|
|
|
6. Упорядоченная таблица-вектор: определение, основные операции, особенности их реализации.
(Определение таблиц - см. билет 4)
(Алгоритмы и структуры данных, лекция 31.03.2004)
Упорядоченные таблицы:
Упорядоченные таблицы - таблицы, элементы в которых упорядочены по значениям ключей (k1<k2<...<kn).
Недостаток: При операциях вставки/удаления необходимо перемещатьинформацию.
Основные операции:
1.Поиск: Для поиска элементов в таких таблицах используется алгоритм "половинного деления". Максимальное время поиска в таких таблицах: log2N.
2.Для динамических упорядоченных таблиц включение элементов и удаление существующих элементов не должно вызывать нарушение структуры таблицы, поэтому при выполнении вставки/удаления необходима реорганизация таблицы.
2.1.Удаление. В результате поиска элемента получаем его индекс в таблице, после чего смещаем нижнюю половину таблицы на 1 позицию вверх.
2.2.При включении нового элемента в таблицу, удобно использовать алгоритм сортировки вставками (при этом сравнение ключей производится от конца таблицы к её началу). При этом, если в таблице не могут находится элементы
с одинаковым значением ключей, сначала необходимо провести поиск в таблице, и, в случае неуспешного поиска, вставить в таблицу новый элемент.
Алгоритм сортировки вставками:
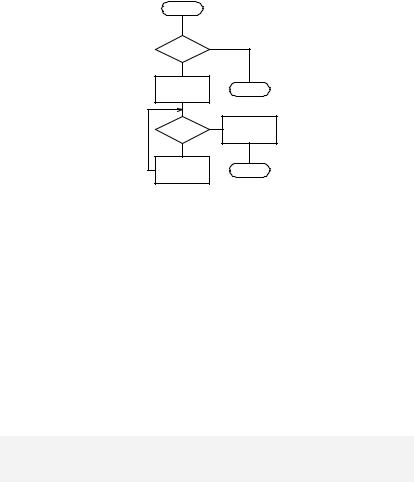
|
|
|
1 |
2 |
|
|
A |
|
inssort |
|
|
|
B |
|
есть место |
нет |
|
|
|
|
да |
|
|
|
C |
|
i = n-1 |
отказ |
|
|
D |
|
i >= 0 и |
нет tabi+1 = новый |
|
|
|
ki > k* |
элемент |
|
|
|
|
|
|
||
|
|
|
да |
|
|
|
E |
|
tabi+1 = tabi |
успех |
|
|
|
i = i-1 |
|
||
|
|
|
|
|
|
Пример реализации: |
/* максимальный размер таблицы |
*/ |
|||
const int M = 20 |
|||||
struct Item{ |
|
|
|
|
|
|
int key; |
|
|
|
|
}; |
Type info; |
|
|
|
|
|
|
|
|
|
|
Item bintable[M]; |
|
*/ |
|
|
|
int n; |
/* текущий размер таблицы |
|
|
||
int inssort(int k, Type in)
{
int i;
for(i = n-1; i >= 0 && bintable[i].key > k; i--) bintable[i + 1] = bintable[i];
bintable[i + 1].key = k; bintable[i + 1].info = dupl(in); return ++n;
}
int insert(int k, Type in)
{
if(binsearch(k) >= 0) |
/* в таблице есть элемент с указанным ключом */ |
return -1; |
|
if(n == M) |
/* в таблице нет свободной позиции для нового элемента*/ |
return -2; |
|
return inssort(k, in); |
|
}
7. Таблица произвольного доступа: определение, основные операции, отображение в памяти. Функция рандомизации, её назначение.
(Алгоритмы и структуры данных, лекция 31.03.2004)
Таблицы с вычисляемыми входами:
Часто операции включения и поиска информации в таблице основываются на использовании не самого ключа, а некоторой информации, зависящей от ключа – так называемого производного ключа. При этом определяется некоторая функция расстановки I(k), которая для заданного ключа k позволяет получить более простой и более эффективный производный ключ, используемый для обращения к элементам таблицы. Обычно производный ключ определяет размещение искомого элемента в таблице. Таблицы, доступ к которым осуществляется с помощью такого производного ключа, называют еще таблицами с вычисляемыми входами.

Вычисляется место размещения элемента в таблице (для вектора - вычисляется индекс элемента). Таблицы с вычисляемыми входами всегда - либо полностью, либо частично - представлены вектором.
Отображение множества ключей на множество индексов:
1.Однозначное отображение. Таблицы произвольного доступа (Random Access).
2.Не однозначное отображение. Пример: шэш-таблицы (перемешанные таблицы). По способу перемешивания делятся:
2.1.Перемешивание сложением;
2.2.Перемешивание сцеплением.
Таблицы произвольного доступа:
Однозначное отображение ключа в индекс.
Особенности:
1.Ключи не хранятся в векторе.
2.Невозможно подобрать функцию рэндомизации для произвольного множества ключей. Применимо только для фиксированного множества ключей (для статических таблиц).
3.Таблицы являются сильно разреженными.
Таблицы произвольного доступа - самые быстрые, но на практике встречаются крайне редко. Главная проблема - подбор функции расстановки.
Свойства таблиц прямого (произвольного) доступа:
1.Так как в таких таблицах ключи элементов однозначно отображаются в элементы вектора, нет необходимости хранить в них значения ключей;
2.В силу сложности подбора функции расстановки часто таблицы прямого доступа имеют не очень высокую степень заполненности таблицы σ , которую можно
определить следующим образом: σ = MN , где M – общее количество элементов,
размещенных в таблице (размер таблицы), N – размер вектора, на который отображается таблица. Обычно σ < 1 и даже (достаточно часто) могут иметь случаи, когда σ << 1.
3.Подбор функции расстановки, обеспечивающей однозначность преобразования ключа элемента таблицы в адрес (индекс) его хранения, в общем случае является очень сложной задачей. На практике ее можно решить только для статических таблиц с заранее известным набором значений ключа. В противном случае при появлении нового ключа k* может возникнуть недопустимая для таких таблиц
ситуация, при которой I(k*) = I(kj) для уже имеющ егося в таблице элемента с ключом kj.
8.Перемешанная таблица: определение, основные операции, хэш-функции, возникающие проблемы, способ отображения в памяти.
(Таблицы с вычисляемыми входами - см. билет 7) (Алгоритмы и структуры данных, лекция 14.04.2004)
Перемешанные таблицы:
Поскольку взаимную однозначность преобразования ключа в адрес хранения элемента таблицы в общем случае обеспечить практически невозможно, от требования взаимной
однозначности отказываются. Это приводит к тому, что для некоторых ki ≠ kj возможна ситуация, что I(ki) = I(kj). Такая ситуация создает переполнение позиций отображаемого
вектора и носит название коллизии (Коллизия - когда два различных ключа отображаются в одну позицию). Чтобы таких коллизий было меньше, функцию расстановки подбирают из условия возможно более равномерного отображения ключей в адреса хранения.
Таблицы, построенные по такому принципу, также являются таблицами с вычисляемыми входами и называются перемешанными. Часто перемешанные таблицы называют еще хэш таблицами (от английского hash – мешанина, путаница), функции расстановки – хэш функциями, а нахождение места хранения элемента – хешированием.
Отличие от таблиц произвольного доступа:
Перемешанную таблицу можно заполнять и обращаться с ней как с таблицей произвольного доступа до тех пор, пока не возникает коллизия. Перемешанные таблицы допускают коллизии, поэтому необходимо хранение в элементе не только информации, но и ключей (в отличии от таблиц произвольного доступа).
Разрешение коллизий:
Проблема состоит в определении места для хранения нового элемента таблицы с ключом kj. Решение этой проблемы предполагает разрешение коллизии и носит название перемешивания (что и определяет название данного типа таблиц – перемешанные). Существуют различные методы перемешивания, зависящие от того, какой способ используется для разрешения коллизии:
•открытое перемешивание (этот способ называют еще перемешиванием сложением см. билет 9);
•перемешивание сцеплением (см. билет 10).
Вперемешанной таблице можно выделить две области: основную, в которую элементы
таблицы отображаются в результате вычисления производного ключа, и область переполнения, в которую попадают элементы в результате перемешивания при обнаружении коллизии. В зависимости от используемого способа перемешивания такое разделение может быть явным или скрытым. В любом случае основная область перемешанной таблицы отображается вектором. Область переполнения может быть отображена и вектором, и списком (точнее, семейством списков), в зависимости от того, какой способ перемешивания используется.
Особенности:
1.Часть таблицы должна отображаться вектором.
2.Пока не появляется коллизия, проблем с размещением элементов не возникает. При возникновении коллизии - вопрос: где размешать элементы-синонимы.
3.Проблема поиска шэш-функции
Замечания:
1.Алгоритм перемешивания при вставке и при поиске должен быть одним и тем же.
2.Основная задача: уменьшение времени поиска. В среднем, время поиска меньше, чем в просматриваемой таблице.
3.Перемешанную таблицу очень легко сделать динамической.
Вопросы к хэш-таблицам:
1.Организация таблицы
1.1.Основная область (вектор)
1.2.Область переполнения (вектор или список)
2.Где размещать? (способ перемешивания)
