2.4.2. Определение модуля и числа зубьев.
-
коэффициент формы зуба. Для седьмой
степени точности
(см.
рекомендацию [1]).
Определим
-
окружной модуль на внешнем торце
конических колес по формуле:
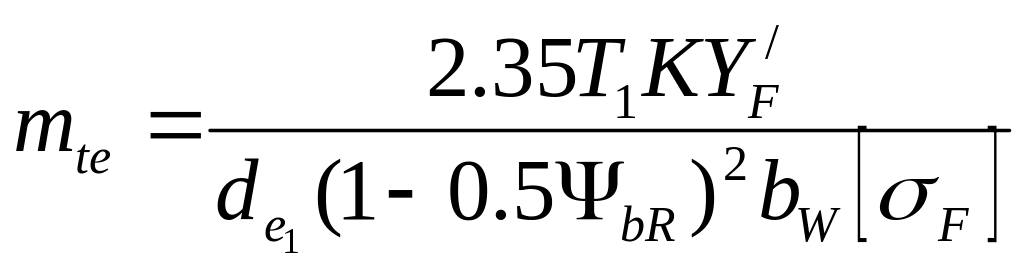
Число
зубьев шестерни
.
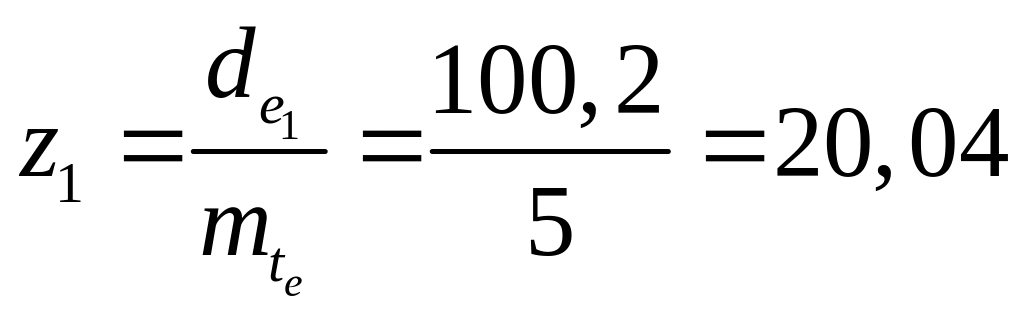Примем
.
Число
зубьев колеса
.
Примем
.
Определим
передаточное число
:
.
Относительное
отклонение полученного передаточного
числа от принятого определим по формуле:
;
.
Определим
-
окружной модуль на середине ширины
зубчатого венца конического колеса:
Определим
средний делительный диаметр шестерни
:
2.4.3. Проверочный расчет передачи на контактную прочность.
Определим
окружную скорость V
по формуле
:
.
-
коэффициент динамической нагрузки
определим по рекомендации [1] (см.
приложение 5, стр.25).
-
коэффициент ширины зубчатого венца
относительно нормального диаметра
шестерни:
-
коэффициент концентрации нагрузки
-
коэффициент неравномерности нагрузки
по ширине колеса. Т.к. HB>350,
то
,
согласно рекомендации [1]. Шестерня
расположена симметрично относительно
опор, следовательно, согласно рекомендации
[1] (см. приложение 5, стр. 25), имеем
.
Тогда
.
Определим
расчетное контактное напряжение
:
;
.
2.4.4. Проверочный расчет передачи на выносливость по изгибу.
Эквивалентное
число зубьев шестерни:
.
Примем
.
Эквивалентное
число зубьев колеса:
,
где
.
.
Примем
.
Определим
и
из рекомендации [1] (см. приложение 9,10,
стр.28).
;
Напряжения
по изгибу определяем по формуле
,
где
.
Определим
расчетные напряжения по изгибу для
шестерни:
Расчетное
напряжение по изгибу для колеса:
Из
предыдущих расчетов
и
.
Следовательно,
и
.
2.4.5. Проверочный расчет передачи на статическую прочность при перегрузках.
Определим максимальное расчетное контактное напряжение
,
где
,
.
Следовательно,
получим:
.
Определим
максимальное контактное напряжение
исходя из условий обработки. При
цементации имеем
-
условие выполняется.
Определим
максимальное допустимое напряжение по
изгибу
:
,
.
Определим
максимальное допустимое напряжение по
изгибу
.
При
имеем:
.
-
условие выполняется.
2.4.6. Определение геометрических размеров передачи.
Внешний делительный диаметр для шестерни:
.
Примем
Внешний делительный диаметр для колеса:
.
Примем
Внешнее
конусное расстояние
.
Примем
.
Среднее
конусное расстояние
.
Примем
Средний делительный диаметр шестерни:
.
Примем
Средний делительный диаметр колеса:
.
Примем
Внешняя
высота головки зубьев:
.
Внешняя
высота ножки зубьев:
.
Угол
ножки зубьев:
Из
предыдущих расчетов
,
.
Угол конуса вершины шестерни и колеса
соответственно:
,
.
Угол конуса впадин шестерни, колеса соответственно:
,
.
Внешний
диаметр вершин зубьев:
.
Примем
.
.
Примем
.
Расстояние от вершины конуса до плоскости внешней окружности вершин зубьев шестерни и колеса, соответственно:
.
Примем
.
.
Примем
.