
- •СОДЕРЖАНИЕ
- •ВВЕДЕНИЕ
- •НАЧАЛЬНЫЕ СВЕДЕНИЯ О ПЛИС
- •Интегральные схемы типа FPGA
- •Перестраиваемый логический блок
- •Генераторы логических функций
- •Триггер
- •Блоки ввода/вывода сигналов
- •Программируемые соединения
- •Динамические параметры конфигурируемого логического блока
- •ОРГАНЫ УПРАВЛЕНИЯ УНИВЕРСАЛЬНОГО ЛАБОРАТОРНОГО СТЕНДА
- •ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
- •Список литературы
- •ВВЕДЕНИЕ
- •ПРОЕКТИРОВАНИЕ ОДНОВЫХОДНОЙ КОМБИНАЦИОННОЙ СХЕМЫ
- •СИНТЕЗ КОМБИНАЦИОННЫХ МНОГОВЫХОДНЫХ СХЕМ
- •Реализация булевых функций с помощью постоянного запоминающего устройства
- •ПРОЕКТИРОВАНИЕ КОМБИНАЦИОННЫХ СХЕМ НА VHDL
- •ПОДГОТОВКА К ВЫПОЛНЕНИЮ РАБОТЫ
- •ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
- •ОТЧЕТ ПО РАБОТЕ
- •Список литературы
- •ВВЕДЕНИЕ
- •СИНХРОННЫЕ ТРИГГЕРЫ СО СТАТИЧЕСКИМ УПРАВЛЕНИЕМ ЗАПИСЬЮ
- •СИНХРОННЫЕ ДВУХСТУПЕНЧАТЫЕ ТРИГГЕРЫ
- •СИНХРОННЫЕ ТРИГГЕРЫ С ДИНАМИЧЕСКИМ УПРАВЛЕНИЕМ ЗАПИСЬЮ
- •УСЛОВНОЕ ГРАФИЧЕСКОЕ ОБОЗНАЧЕНИЕ ТРИГГЕРНЫХ СХЕМ
- •ПРОЕКТИРОВАНИЕ ТРИГГЕРНЫХ СХЕМ
- •ПРОЕКТИРОВАНИЕ СИНХРОННЫХ ДВУХСТУПЕНЧАТЫХ ТРИГГЕРОВ
- •ПОСТРОЕНИЕ СИНХРОННЫХ ТРИГГЕРОВ С ДИНАМИЧЕСКИМ УПРАВЛЕНИЕМ ЗАПИСЬЮ
- •ПРОЕКТИРОВАНИЕ ТРИГГЕРНЫХ СХЕМ НА VHDL
- •ПОДГОТОВКА К ВЫПОЛНЕНИЮ РАБОТЫ
- •ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
- •ОТЧЕТ ПО РАБОТЕ
- •Список литературы
- •ВВЕДЕНИЕ
- •СИНТЕЗ СИНХРОННЫХ СЧЕТЧИКОВ
- •Матрица переходов триггера
- •ПРИМЕР
- •ПРОЕКТИРОВАНИЕ СЧЕТЧИКОВ НА VHDL
- •ПОДГОТОВКА К ВЫПОЛНЕНИЮ РАБОТЫ
- •ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
- •ОТЧЕТ ПО РАБОТЕ
- •Список литературы
- •ВВЕДЕНИЕ
- •ПРОЕКТИРОВАНИЕ МНОГОФУНКЦИОНАЛЬНОГО РЕГИСТРА
- •ДИНАМИЧЕСКИЕ ПАРАМЕТРЫ РЕГИСТРОВ
- •ПРОЕКТИРОВАНИЕ РЕГИСТРА НА VHDL
- •ПОДГОТОВКА К ВЫПОЛНЕНИЮ РАБОТЫ
- •ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
- •ОТЧЕТ ПО РАБОТЕ
- •Список литературы
- •ВВЕДЕНИЕ
- •Статические и динамические состязания сигналов
- •Функциональные и логические состязания сигналов
- •Синтез схем, свободных от логических состязаний
- •Анализ комбинационных схем с целью выявления состязаний
- •СОСТЯЗАНИЯ СИГНАЛОВ В ПОСЛЕДОВАТЕЛЬНОСТНЫХ СХЕМАХ
- •Последовательностные схемы
- •Условия надежного функционирования асинхронной схемы
- •Критические состязания
- •Существенные состязания
- •Анализ асинхронных последовательностных схем
- •Устранение критических состязаний
- •ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ СОСТЯЗАНИЙ СИГНАЛОВ
- •ПОДГОТОВКА К ВЫПОЛНЕНИЮ РАБОТЫ
- •ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
- •ОТЧЕТ ПО РАБОТЕ
- •Список литературы
- •Логические элементы
- •Мультиплексоры
- •Описание цифрового осциллографа
- •Запуск и настройка осциллографа
- •Настройка изображения сигнала на экране осциллографа
- •Получение устойчивого изображения сигнала
- •Выбор цены деления по оси Х и Y
- •Выбор фронта сигнала по входу Х осциллографа
- •Измерение временных интервалов (измерение задержек)

ставляют собой сумму соответствующих задержек логических элементов, входящих в путь;
наконец, определяют числовое значение задержек комбинационной схемы, подставляя в найденные выражения значения задержек логических элементов.
Для спроектированной комбинационной схемы (см. рис. 2.2) наиболее длинный путь содержит три элемента. Таких путей в схеме несколько:
D1→D3→D7, D1→D4→D7, D1→D5→D7 и D2→D6→D7.
На временной диаграмме существует несколько состояний, переход к которым активизирует некоторые из этих путей. Можно выбрать любые из них для оценки задержек переключения комбинационной схемы. Два перехода с обозначением задержек элементов показаны на рис. 2.3.
Непосредственно из рис. 2.3 можно записать выражения для задержек переключения выходного сигнала комбинационной схемы:
tз01.КС = tз01.D1 +t10з.D4 +tз01.D7 , t10з.КС = t10з.D1 +tз01.D5 +t10з.D7 .
Подставляя в найденные выражения паспортные значения задержек логических элементов, получим числовое значение задержек комбинационной схемы.
СИНТЕЗ КОМБИНАЦИОННЫХ МНОГОВЫХОДНЫХ СХЕМ
На практике относительно редко встречаются комбинационные схемы с одним выходом, т.е. реализующие одну функцию. Обычно схемы имеют несколько выходов, причем значения сигналов на всех выходах зависят от одних и тех же входных сигналов. Работа комбинационной схемы, имеющей п входов и k выходов, описывается совокупностью k функций (2.1), каждая из которых определяет закон функционирования схемы по одному выходу.
Если провести минимизацию переключательных функций, входящих в совокупность, независимо друг от друга, то схема с многими выходами, реализующая эти функции, будет содержать k изо-
28

лированных цепей. Однако в общем случае схему можно существенно упростить за счет объединения участков схемы, реализующих одинаковые члены (или группы членов), содержащиеся в нескольких переключательных функциях.
Например, реализация двух функций в МДНФ
f1 = x1 x3 x1 x2 ; f 2 = x1 x2 x3 x1 x2
потребует применения четырех элементов И и двух элементов ИЛИ. Если же первую из них представить в виде
f1 = x1 x2 x3 x1 x2 ,
то, отказываясь от минимального представления, но не изменяя значения функции (это легко проверить, например, по диаграмме Вейча), можно упростить реализацию, поскольку первый член является общим для обеих функций. В этом случае потребуется три элемента И и два элемента ИЛИ.
Из этого примера следует, что задача минимизации для системы переключательных функций не может быть сведена к задаче минимизации отдельных функций.
Общая идея минимизации схем с многими выходами сводится к получению таких выражений для совокупности переключательных функций, в которых оптимально используются члены, общие для нескольких функций.
Минимизация системы логических функций
Рассмотрим один из методов совместной минимизации системы логических функций — метод меток [1-4].
Данный метод предусматривает выполнение следующих этапов:
нахождение всех простых импликант системы логических функций;
определение простых импликант для минимального представления системы логических функций;
запись каждой логической функции в дизъюнктивной нормальной форме.
29

Нахождение всех простых импликант системы логических функций
Пусть даны три функции, каждая из которых зависит от четырех переменных:
F1 (A, B, C, D) =∑(0, 2, 4, 6,10,12,14), |
|
|
F2 (A, B, C, D) =∑(2, 3,10), |
|
(2.4) |
|
||
F3 (A, B, C, D) =∑(0,1, 2, 3, 9,11). |
|
|
|
|
|
Простые импликанты системы логических функций (2.4) представляют собой совокупность простых импликант всех сочетаний логических произведений исходных функций, включая и функции системы: F1, F2, F3, F1 F2, F1·F3, F2·F3 и F1·F2·F3.
Таким образом, сначала находят все простые импликанты каждой функции системы F1, F2, F3. Затем из функций системы образуют все возможные подсистемы, состоящие из двух функций: F1 F2, F1·F3, F2·F3. Для каждой из полученных подсистем функций находят все простые импликанты. Затем образуют подсистему из трех функций F1·F2·F3 и для нее находят все простые импликанты.
Эту процедуру удобнее всего выполнить, используя диаграммы Вейча. Занесем исходные функции на три диаграммы Вейча
(рис. 2.4).
Рис. 2.4. Диаграммы Вейча трех функций
30
Найдем все простые импликанты для этих функций, т.е. сокращенную дизъюнктивную нормальную форму (СкДНФ) функций F1,
F2, F3:
F1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= BD |
|
CD AD, |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F2 |
= BCD ABC, |
|
|
(2.5) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F3 |
= BD AB. |
|
|
|||||||||||||||||
|
|
|
||||||||||||||||||
Затем необходимо найти СкДНФ функций, представляющих собой все сочетания логических произведений исходных функций:
F1·F2, F1·F3, F2·F3 и F1·F2·F3.
Получение логического произведения функций легко осуществить с помощью диаграммы Вейча. Для этого необходимо совместить диаграммы Вейча соответствующих функций. Затем в каждой клетке совмещенной диаграммы выполнить операцию конъюнкция над значениями совмещаемых функций. Данная операция показана на рис. 2.5 для функции F1·F2.
На этом же рисунке представлены диаграммы Вейча и для остальных логических произведений исходных функций.
По полученным диаграммам найдем простые импликанты данных функций:
F1 F2 = |
|
|
|
|
|
|
, |
|
|
|
|
|||||
B |
CD |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F1 F3 = ABD, |
|
|
|
(2.6) |
||||||||||||
F2 F3 = |
|
|
|
|
C, |
|
|
|
||||||||
A |
|
B |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
F1 F2 F3 = ABCD. |
|
|||||||||||||||
31
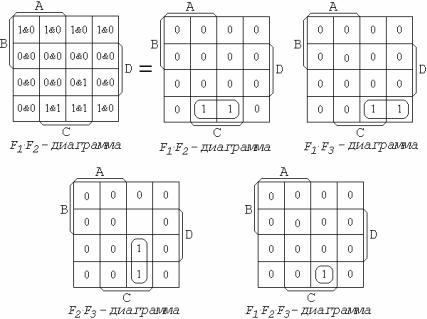
Рис. 2.5. Диаграммы Вейча логических произведений трех функций
Определение простых импликант для минимального представления системы логических функций
На втором этапе минимизации из полученных простых импликант путем перебора различных вариантов отыскивают наиболее простые формулы для представления системы функций. Отыскание таких формул удобно производить с помощью импликантной матрицы для системы функций [2, 3]. По импликантной матрице выбирают совокупность простых импликант, которая поглощает все конституенты системы логических функций. Такую совокупность простых импликант принято называть полной. Из всех полных систем импликант выбирают ту, которая содержит наименьшее число букв (так называемую минимальную полную совокупность).
32

Составление импликантной матрицы системы функций
Импликантная матрица системы функций составляется следующим образом (табл. 2.1). В заголовке строки матрицы записывают одну из простых импликант системы функций (2.5) и (2.6) с мет-
кой.
Метка импликанты — это имена функций, участвовавших в ее образовании.
Например, импликанта BD из системы функций (2.5) получит метку F1, а BD — метку F3; а импликанта BCD из системы (2.6) будет иметь метку F1F2 (см. табл. 2.1).
Примечание. Одна и та же импликанта может присутствовать как в системе функций (2.5), так и в системе (2.6). В этом случае импликанта записывается один раз с наиболее длинной меткой.
В заголовке столбцов матрицы записывают все конституенты единицы системы логических функций. Каждой конституенте единицы будем приписывать метку, указывающую, в какие функции входит данная конституента; для каждого признака (метки) конституенты отводится отдельная колонка (см. табл. 2.1). Например,
конституента единицы ABCD имеет метку F1F2, так как она входит в функцию F1 (A, B, C, D) и F2 (A, B, C, D), а в функцию F3 (A, B, C, D) не входит (см. систему уравнений (2.4)).
Каждая клетка импликантной матрицы соответствует конституенте с признаком и простой импликанте. Если конституента поглощается импликантой и признак конституенты содержится в признаке импликанты, то соответствующая клетка отмечается кре-
стиком. Например, на пересечении строки с импликантой ABD F1F3 и столбца с конституентой ABCD крестиками отмечаются только седьмая и девятая колонки, содержащие метки F1 и F3
(см. табл. 2.1).
33

Выбор подмножества импликант с минимальным числом букв
Заданные логические функции могут быть построены из любой совокупности импликант, совместно перекрывающих все колонки импликантной матрицы. Задача состоит в выборе подмножества импликант с минимальным числом букв. Для выбора такого подмножества прежде всего найдем колонки с меткой Fi и конституентой Кj, имеющие единственный крестик. Соответствующая данному крестику импликанта должна обязательно входить в функцию Fi, так как только она поглощает конституенту Кj.
В табл. 2.1 колонки с номерами 1, 6, 12, 14 и 15 имеют единственный крестик. Соответствующие этим крестикам импликанты отмечены в табл. 2.1 символом « √ ». Этим же символом отмечены внизу табл. 2.1 все колонки, перекрытые выбранными импликантами.
После этого найдем импликанты, перекрывающие остальные колонки. В рассматриваемом примере такой выбор осуществляется тривиально, так как неотмеченными остаются колонки 10, 11, ко-
торые перекрываются одной импликантой ABD F1F3. Данная импликанта и перекрываемые ею колонки отмечены в табл. 2.1 символом « ».
Набор отмеченных простых импликант, перекрывающих совместно все колонки импликантной матрицы, будет полным подмно-
жеством дизъюнктивных членов заданной совокупности логиче-
ских функций.
34
Таблица 2.1
Импликантная матрица системы логических функций
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Конституента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Импликанта |
ABC |
D |
|
ABCD |
|
|
A |
BCD |
|
ABCD |
|
ABCD |
|
ABCD |
|
ABCD |
ABCD |
ABCD |
ABCD |
ABCD |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F1 |
|
F1 |
|
|
|
F1 |
|
|
|
F1 |
|
F1 |
F2 |
F1 |
|
|
|
F2 |
|
F3 |
F1 |
F3 |
F2 |
F3 |
|
F3 |
|
F3 |
|
|
|
F3 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
6 |
|
7 |
|
8 |
|
|
9 |
10 |
11 |
12 |
13 |
14 |
|
15 |
16 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
A |
|
|
B |
CD |
|
F1F2F3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
+ |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C F2F3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
+ |
|
|
|
|
|
|
|
+ |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
√ |
A |
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F1F3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
+ |
+ |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
A |
B |
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F1F2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
+ |
+ |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
B |
CD |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
√ |
|
|
|
|
|
D |
|
F3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
+ |
|
+ |
+ |
|
||||||||||||||||||||||||||
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
+ |
|
|||||||||||||
|
|
|
|
A |
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F1 |
+ |
|
|
+ |
|
|
+ |
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
√ BD |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F1 |
|
|
|
|
+ |
|
|
+ |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
CD |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
F1 |
|
|
|
|
|
|
|
+ |
|
|
+ |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
A |
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
√ |
|
|
|
√ |
|
|
|
√ |
|
√ |
√ |
√ |
√ |
√ |
|
|
√ |
√ |
|
√ |
|
√ |
|
|
|
√ |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Запись логических функций в ДНФ
С помощью импликант найденного подмножества нетрудно записать каждую логическую функцию в дизъюнктивной нормальной форме. Для этого достаточно составить дизъюнкцию тех отмеченных импликант, которые совместно перекрывают все колонки, содержащие метку данной функции. Выбирая для каждой функции минимально возможное количество отмеченных импликант, получаем искомую минимальную совокупность переключательных функций:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|||||||
F1 (A, B,C, D) = BD |
B |
CD |
A |
B |
D |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F2 (A, B,C, D) = BCD ABC, |
|
|
|
|
|
|
(2.7) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F3 (A, B,C, D) = BD ABD. |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
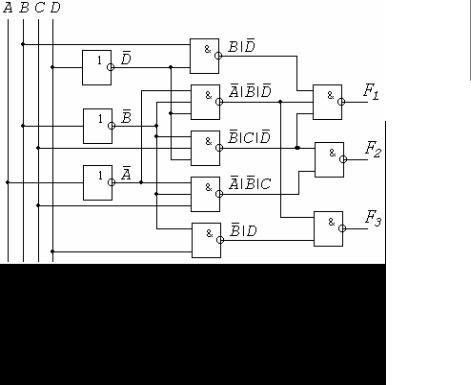
На рис. 2.6 приведена реализация системы функций (2.7) на элементах И-НЕ.
Рис. 2.6. Реализация многовыходной комбинационной схемы
36
