Рис. 6.16. Cхема, свободная от критических состязаний сигналов

Изложенный материал далеко не исчерпывает всех проблем, связанных с состязаниями в цифровых схемах, однако может помочь во многих случаях обнаружить состязания и принять меры по их устранению.

ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ СОСТЯЗАНИЙ СИГНАЛОВ

Экспериментальное исследование состязаний сигналов в цифровых схемах проводится как с помощью моделирования, так и на универсальном лабораторном стенде.

Исследование комбинационной схемы

Исследование состязаний сигналов в комбинационной схеме выполняется только моделированием с использованием единичных задержек элементов. Для этого необходимо задать на входах комбинационной схемы переходы между всеми парами состояний, вызывающих состязания сигналов.

168

Исследование последовательностной схемы

Для исследования состязаний сигналов в последовательностной схеме необходимо подать на ее вход полную последовательность смежных входных состояний x1,x2 : 00 → 01 → 11 → 10 → 00 → 10 → 11 → 01 → 00 и т.д.

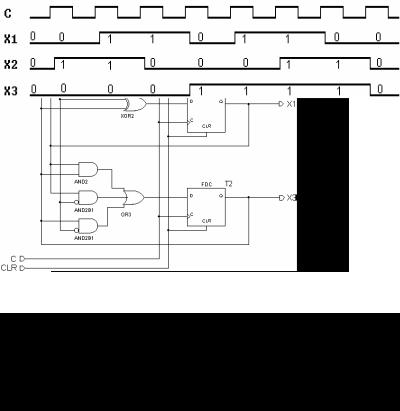
Данную последовательность вырабатывает схема, изображенная на рис. 6.17. Временная диаграмма ее работы приведена на рис. 6.18.

Рис. 6.17. Генератор последовательности смежных состояний х1, х2

Рис. 6.18. Временная диаграмма генератора последовательности смежных состояний х1, х2

169

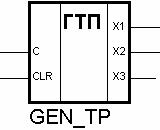
Схема генератора тестовой последовательности сигналов х1, х2 оформлена в виде макроэлемента, условное графическое обозначение которой приведено на рис. 6.19. Данный макроэлемент содержится в библиотеке проекта maket.

Доступность выходного сигнала Х3 макроэлемента облегчает выделение периода работы исследуемой схемы на временной диаграмме при моделировании, а также данный сигнал необходим для синхронизации осциллографа при выполнении эксперимента на лабораторном стенде.

Рис. 6.19. Условное графическое обозначение генератора тестовой последовательности смежных состояний х1, х2

Исследование заданной асинхронной схемы выполняют как моделированием в САПР Xilinx, так и на универсальном лабораторном стенде.

Построение ленты схемы

С целью фиксации ошибочного перехода исследуемой схемы из-за состязаний сигналов необходимо заранее по таблице переходов и выхода определить реакцию схемы на заданную полную последовательность смежных входных состояний (см. рис. 6.18).

В табл. 6.6 приведена заданная последовательность входных сигналов и соответствующие ей последовательности состояний внутренних переменных и выхода для схемы рис. 6.9. Закон функционирования этой схемы определен табл. 6.1. Табл. 6.6 называют лентой схемы. Ленту схемы строят по кодированной таблице пере-

170

ходов (см. табл. 6.1), определяя возможные переходы при изменении входного состояния.

После включения питания и установки в нулевое состояние генератора последовательности x1,x2 исследуемая схема может оказаться в одном из двух устойчивых состояний y1 y2 z = 101 или y1 y2 z = 110 (см. табл. 6.1). При составлении табл. 6.6 за начальное принято состояние схемы y1 y2 z = 1ХХ.

Из табл. 6.1 определяем переходы с критическими состязаниями и фиксируем в табл. 6.6 возможные ошибочные переходы.

Для рассматриваемого примера схема из ошибочного состояния вновь переходит в русло правильной работы (см. табл. 6.1). В общем случае после ошибочного перехода последовательность состояний схемы может отличаться от правильной. В этом случае в ленте фиксируют как правильную последовательность состояний схемы, так и последовательность состояний после ошибочного перехода.

Как видно из табл. 6.6, после первого завершения периода входной последовательности схема переходит в состояние y1 y2 z = 110, которое отлично от исходного состояния y1 y2 z = 1ХХ01. Поэтому необходимо продолжить построение ленты исследуемой схемы до выделения периода работы схемы. Это необходимо для исследования работы схемы в динамическом режиме.

Поскольку после второго периода входной последовательности схема переходит в состояние y1 y2 z = 110, т.е. совпадает с состоянием схемы в начале этого периода, то построение ленты можно завершить (см. табл. 6.6).

171

Таблица 6.6

Моделирование последовательностной схемы

Следует отметить, что при проведении эксперимента ошибочный переход может и отсутствовать. Все зависит от реального соотношения задержек в цепях, определяющих порядок изменения сигналов обратной связи Y1 и Y2.

Для того чтобы убедиться, возможен предсказанный на ленте ошибочный переход или нет, следует:

выполнить моделирование схемы с использованием единичных задержек элементов на полной последовательности смежных входных состояний;

затем реализовать временное моделирование схемы, предварительно подсоединив макроэлементы лабораторного стенда и выполнив размещение проекта на кристалл;

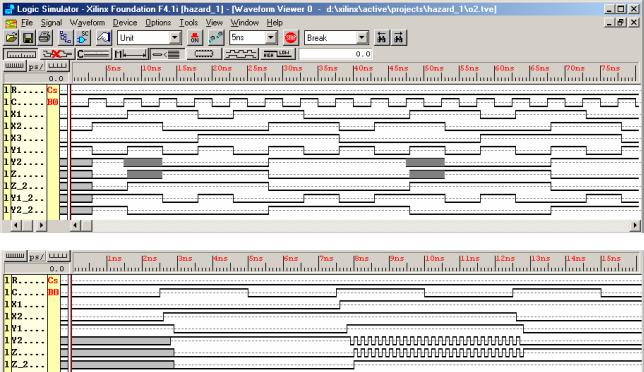
сделать заключение о реальности ошибочного перехода схемы. На рис. 6.20 приведены результаты одновременного моделирования схем, изображенных на рис. 6.9 и 6.16, с единичными задержками элементов. На рис. 6.20(а) временная диаграмма воспроизводит отрезок времени, приведенный в табл. 6.6, а на рис. 6.20(б) — де-

тальный фрагмент указанной временной диаграммы.

Как видно, система моделирования неопределенное состояние элементов схемы в начальный момент времени (x1x2 = 00) отображает светло-серым цветом (см. рис. 6.20).

173

а)

б)

Рис. 6.20. Временные диаграммы работы схемы с единичными задержками элементов