1. Этапы проектирования комбинационных схем на примере дешифратора на 4 выхода: определение, таблица истинности, функция, логическая схема. Увеличение размерности до 16 выходов.

Задача: Реализовать функцию F1(X2,X1,X0)=Ʃ(0,1,4,6,7) на дешифраторе.

ЗАДАЧА: реализовать функциюF1(X2,X1,X0)=Σ(0,1,4,6,7) на дешифраторе.

Этапы проектирования комбинационных схем (?):

1. Составляем таблицу истинности

2. Проводим минимизацию и записываем функцию

3. Переводим функцию в нужный базис и строим схему

4. По схеме стоим временную диаграмму и определяем временные параметры схемы.

Дешифратор Определение:Дешифратор (DC) - комбинационная схема. Она будет иметь n входов и 2ⁿ выходов (полный дешифратор). При любой комбинации поступающих на вход сигналов всегда будет возбуждён только один из выходов. Номер этого возбуждённого выхода будет определяться номером набора.

Функция (списываем с таблицы истинности):

F0=X2*X1; F1=X2*X1; F2=X2*X1; F3=X2*X1.

Логическая схема:схема реализации полного дешифратора 2->4 (дешифратор на 4 выхода)

Увеличение разрядности до 16-ти

Рассмотрим построение полного дешифратора на 16 выходов из дешифраторов 2->4.

При этом для 16-ти выходов число входов будет n=4 (т.к. n 2 16= ).

Для увеличения разрядности дешифратора можно применить каскадную схему из дешифраторов (аналогично схеме на мультиплексорах). При этом на входы E (Enable - разрешение) подаются выходы первого дешифратора.

ЗАДАЧА:реализовать функцию F1(X2,X1,X0)=У(0,1,4,6,7) на дешифраторе.

2. Этапы проектирования комбинационных схем на примере мультиплексора 4-1: определение, таблица истинности, функция, логическая схема. Увеличение размерности до 16-1.

Задача: Реализовать функцию F2(X3,X2,X1,X0) = Ʃ(0,2,6,7,8,9,13,14) на мультиплексоре.

ЗАДАЧА: реализовать функциюF2(X3,X2,X1,X0)=Σ(0,2,6,7,8,9,13,14) на мультиплексоре.

Мультиплексор реализует некоторая комбинационная схема (мультиплексорная схема), которая будет иметь n входов адреса (на которые будут подаваться сигналы n x x ,..., 1 ), 2n входов DI - Data Input (вход данных - информационный сигнал) и один выход DO – это Data Out (выход данных - информационный выход). По существу, эта схема коммутирует 2n входных каналов на выходной канал. Номер коммутируемого канала будет определяться набором сигналов n x x ,..., 1 . Мультиплексор также имеет вход Е–разрешения.

Функция мультиплексора: F _{max (4->1)}=E(A1 A0 D0 v A1 A0 D1v A1 A0 D2 v A1 A0 D3)

DI0 - первый информационный вход. DI1 - второй информационный вход.

При подаче 0 на адресный вход X1, на выход DO будет передаваться сигнал с первого информационного входа DI0; при подаче 1 - со второго информационного входа DI1.

Ниже идет: Реализация логической функции на мультиплексоре. F2(X3,X2,X1,X0)=

Σ(0,2,6,7,8,9,13,14)

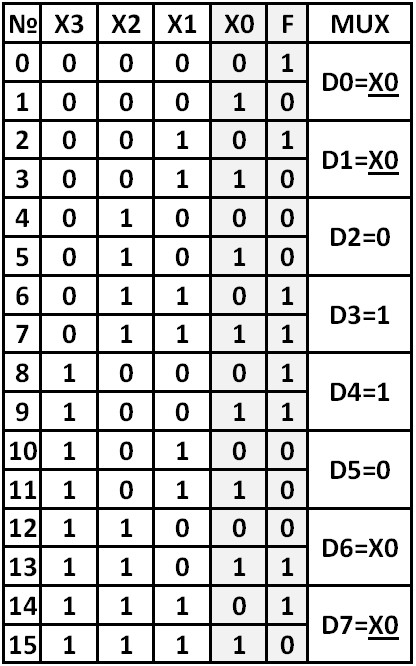
Для увеличение разрядности

мультиплексора с использованием дешифратора,

который по состоянию Х2-

Х3 выбирает один из 4-ех

мультипл-ров 4->1.

3. Этапы проектирования комбинационных схем на примере схемы сравнения двухразрядных слов: определение, таблица истинности, функция, логическая схема. Схема сравнения для четырехразрядных слов на элементах "Исключающее ИЛИ".

Этапы проектирования комбинационных схем (см. билет 1).Функция "исключающее ИЛИ". Выполняет функцию - сумма по модулю два (он же называется ещё и "управляемым инвертером"). Ноль на выходе будет только в случае равенства двух операндов.

"Исключающее ИЛИ": (двухвходовая схема) на выходе будет 0 только в случае равенства операндов на входе

Управляемая инверсия: если считать, что а - это управляющий вход (см. схему), то получается, что при 0 передаём b напрямую, при 1 - инвертируем.

Сравнение двухразрядных слов (на исключающих ИЛИ):

Определение: Схема сравнения - это логическая комбинационная схема, на выходе

которой ноль будет только в случае равенства операндов.

Таблица истинности (0 будет там, где значения операндов A и B равны):

То есть - сначала поразрядно сравниваются операнды, и если хотя бы один из разрядов не совпадает (результат сравнения =1), то и числа в целом не равны (эта единица должна пойти на выход). То есть - сначала должны быть элементы "Исключающее ИЛИ", а далее элемент "ИЛИ" (где - если хотя бы одна единица на входе, то на выходе будет 1). Получаем следующую функцию: где A0 - младшие разряды первого операнда, A1 - старшие (аналогично для второго операнда B).Логическая схема (по функции):

Схема сравнения четырех разрядных слов (на искл. ИЛИ):

Функция (по аналогии с двумя операндами):

Функция (для реализации на ТТЛ-микросхем):

4. Сумматор: определение, таблица истинности одноразрядного сумматора, функции суммы и переноса, логическая схема, временные параметры. Схема 4-х разрядного сумматора с последовательным переносом, время суммирования.

Сумматор- это некоторый элемент, который выполняет операцию арифметического суммирования двух чисел (суммирование может быть ещё и логическое). Сумматор производит над словами некоторые операции. Значение суммы, которая образуется на выходе нашего сумматораS(S_n;S_(n-1); … ;S₁); в общем случае рассматривается операция над двумя словами:x(x_n;x_(n-1); … ;x₁) иy(y_n;y_(n-1);…;y₁)

Таблица истинности (справа) одноразрядного сумматора: (Zi- перенос из предыдущего разряда.)

Классификация сумматоров(возможно не нужна):

1. По количеству входов: a. 2 входа (полусумматор) обозначается HS; b. 3 входа (полный сумматор) обозначается S (Sum)	2. По способу организации процесса суммирования: a. одноразрядные/многоразрядные; b. комбинационного типа/накапливающего типа.
3. По способу последовательности разрядов суммируемых слов; a. с младших разрядов; b. со старших разрядов.	4. По наличию тактовых импульсов: a. синхронный; b. асинхронный. По переносу (многоразрядные сумматоры): групповой, последовательный, сквозной, параллельный.

Функции суммы и переноса.

Если q – основание системы счисления, i S – сумма i-го разряда, аi P –перенос из i-го разряда,1 . i P - перенос из предыдущего разряда. то можно записать следующие

функции для суммы и переноса:

если: x_i + y_i + P_i-1 < q, то S_i = x_i + y_i +P_i-1 и P_i=0;

если: x_i + y_i + P_i-1 >= q, то S_i = x_i + y_i +P_i-1 – q и P_i=1;

Минимизация по диаграммам Вейча

Временные параметры.

У сумматора есть 6 временных параметров:

Но так как путь A->S равен B->S и A->Р равен B->Р, то можно записать четыре характеристики, если есть входные данные A и B: 1) от AB до суммы: AB->S, 2) от AB до переноса: AB->P, 3) от входного переноса до суммы: P->S, 3) от входного переноса до выходного переноса: P->P.

Схема 4-х разрядного сумматора с последовательным переносом, время суммирования. У многоразрядного сумматора с последовательным переносом (перенос от разряда к разряду) время суммирования будет равноSum=t_ap+(n-2)t_pp+t_ps. В нашем случае n=4. Схема такого сумматора состоит из 4-х сумматоров, у которых выходной перенос предыдущего разряда соединен со входным переносом следующего разряда.