18.3.4. Критерий устойчивости Михайлова

Применение критерия устойчивости Гурвица для систем с характеристическим уравнением выше 4-го порядка затруднено.

Частотный критерий устойчивости А.М.Михайлова позволяет судить об устойчивости систем любого порядка по виду ее характеристического вектора (годографа) на комплексной плоскости. Годограф Михайлова получают подстановкой P=j в характеристический полином характеристического уравнения и построением кривой в координатах U() и jV() при изменении  от 0 до 

D(j)=U()+jV()=a₀(j)ⁿ + a₁(j)^n-1+...+ a_n-1(j)+a_n . (1.6.18)

Определение критерия Михайлова. Для устойчивости ЭЦ необходимо и достаточно, чтобы ее характеристический вектор при изменении частоты от 0 до  повернулся против часовой стрелки, начиная с положительной вещественной оси и проходя последовательно такое количество квадрантов на координатной плоскости, которое равно порядку характеристического уравнения, т.е. угол поворота должен быть n/2.

На рис.1.6.4,а показаны кривые устойчивых систем, а на рис.1.6.4,б - неустойчивых систем.

Рис.1.6.4. Кривые Михайлова: а - устойчивые системы; б - неустойчивые системы

18.3.5. Критерий устойчивости Найквиста

Частотный критерий устойчивости Найквиста базируется на частотных характеристиках разомкнутой цепи системы частотного управления и дает правила, согласно которым по виду частотной характеристики разомкнутой цепи можно судить об устойчивости замкнутой системы.

По критерию Михайлова изменение аргумента должно быть равно n/2. Но если цепь замкнуть, то на выходе и входе должны быть одинаковые аргументы, т.е. argФ(j)=0. Это значит, что амплитудно-фазовая характеристика Ф(j) не должна охватывать начало координат (рис.1.6.6,а). Если рассмат­ривать разомкнутую систему преобразованием из замкнутой, то

W(j)=Ф(j)-1. (1.6.23)

Отсюда получаем амплитудно-фазовую частотную характеристику разомкнутой цепи (рис.1.6.6,б).

Рис.1.6.6. Годографы Найквиста для замкнутой (а), разомкнутой (б) устойчивой САУ и неустойчивой САУ (в)

Определение критерия Найквиста

Замкнутая система устойчива, если амплитудно-фазовая частотная характеристика разомкнутой системы не охватывает на вещественной оси точку с координатой - 1.

Вопросы для контроля:

1. Доказать, что операторная передаточная функция дифференциатора на операционном усилителе равна (–pRC). Построить график АЧХ такого дифференциатора.

2. Определить передаточную функцию цепи, изображенной на рис. 14.9.

Ответ:

3. Что такое годограф петлевого усиления? Как по годографу определить тип обратной связи?

4. Как формулируется критерий устойчивости Найквиста? Для каких цепей он используется?

5. Сформулируйте критерий устойчивости Рауса-Гурвица. Как составить определитель Гурвица? Приведите примеры.

6. Определить комплексную передаточную функцию H_р(j ) цепи на рис. 14.9 разомкнутой обратной связью. Исследуйте зависимость устойчивости цепи от величины коэффициента усиления К.

Ответ:

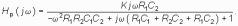
7. В чем геометрический смысл критерия устойчивости Михайлова?

8. Определить относительные изменения коэффициентов усиления трех усилителей, охваченных ООС с коэффициентом передачи H_ос = 0,01, если их коэффициенты усиления без ОС равны H_1у = 5 10²; H_2у = 5 10³; H_3у = 5 10⁴, а относительная стабильность коэффициента усиления составляет 1%.

Ответ: ; ; .
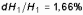