Обобщенная схема автогенератора

 

Схема автогенератора должна содержать активный элемент с нелинейной вольт-амперной характеристикой, колебательную систему (в данном случае контур), внешнюю цепь положительной ОС, по которой колебание с выхода колебательной системы подается на вход активного элемента. Такие автогенераторы являются генераторами с внешней ОС; структурная схема построения таких генераторов приведена на рис. 15.3.

Заметим, что нелинейный активный элемент с колебательной системой образуют нелинейный резонансный усилитель. Поэтому можно представить обобщенную структурную схему автогенератора с разомкнутой цепью обратной связи (рис. 14.17, а). Комплексная передаточная функция всей цепи

H_p(j U_ос(jU_вх(j = H_у(jH_ос(j.

 

Для того, чтобы в генераторе происходило самовозбуждение колебаний, необходимо, чтобы модуль комплексного напряжения  | U_ос(j)| на выходе схемы был больше модуля комплексного напряжения | U_вх(j)| на входе схемы, откуда

   | H_p(j)|  | H_p(j)| ^. | H_ос(j)| > 1. 

При приближении к стационарному режиму модуль комплексного коэффициента передачи усилителя  | H_p(j)| за счет влияния нелинейности начинает уменьшаться до тех пор, пока не наступит динамическое равновесие (см. § 14.3):

 | H_p(j)|  | H_p(j)| ^. | H_ос(j)| = 1. 

Это условие соответствует стационарному режиму и известно под названием баланса амплитуд. Учитывая, что

получаем фазовый сдвиг в разомкнутой цепи автогенератора

_p() = _p() + _ос().

Баланс фаз, т. е. совпадение фаз напряжений на входе и выходе схемы рис. 14.17, а, наступает при_p() = 2. Таким образом, сдвиг фаз в цепи обратной связи зависит от сдвига фаз в усилителе п дополняет его до 2. Если на частоте генерируемых колебаний усилитель вносит сдвиг фаз  _у =2 (как, например, в схеме рпс. 15.2), то цепь обратной связи должна на этой же частоте вносить сдвиг фаз _ос() = . В схеме автогенератора рпс. 15.2 поворот фазы напряженияu_ос(t) на 180° достигается, как ранее отмечалось, соответствующим включением обмоток катушки индуктивности L_ос.

18.3. Устойчивость цепи с обратной связью

Введем понятия устойчивой и неустойчивой цепи. Цепь называется устойчивой, если свободные колебания с течением времени стремятся к нулю. В противном случае цепь называется неустойчивой. Из теории переходных процессов (гл. 6, 7) следует, что цепь является устойчивой, если корни характеристического уравнения лежат в левой полуплоскости комплексной переменной р. Если корни такого уравнения лежат в правой полуплоскости, то цепь является неустойчивой, т. е. она находится в режиме самовозбуждения. Таким образом, для определения условий устойчивости цепи достаточно найти характеристическое уравнение и его корни. Как видим, условия устойчивости можно определить и не вводя понятие обратной связи. Однако здесь возникает ряд проблем. Дело в том, что вывод характеристического уравнения и определение его корней являются громоздкой процедурой особенно для цепей высокого порядка. Введение понятия обратной связи облегчает получение характеристического уравнения или даже дает возможность обойтись без него. Крайне важно и то, что понятие обратной связи адекватно физическим процессам, возникающим в цепи, поэтому они становятся более наглядными. Глубокое понимание физических процессов облегчает работу по созданию автогенераторов, усилителей и т. д.

Классический метод решения дифференциальных уравнений динамики электрических цепейзаключается в получении аналитического выражения общего интеграла уравнения, который определяется суммой

Y(t) = Y_вын + Y_св(t), (1.2.9)

где Y(t) - общее решение, дающее переходной процесс выходной величины в функции времени;

Y_вын - частное решение уравнения, определяющее вынужденное (установившееся) движение для производных равных нулю;

Y_св(t) - решение левой части уравнения (1.2.8), приравненное нулю (характеризует свободное движение).

В частном случае, когда корни характеристического уравнения _i вещественные для характеристического уравнения

, (1.2.10)

получим

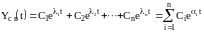, (1.2.11)

где C_i - постоянные интегрирования, _i - корни характеристического уравнения (1.2.10).

Если корни _i мнимые, то в решении (1.2.11) будут и гармонические составляющие, т.е. будет происходить колебательный процесс.

Считают, что САУ устойчива, если свободная составляющая будет затухать, т.е.

. (1.6.4)

Свободная составляющая представляется в решении уравнения (1.2.8) следующим видом:

, (1.6.5)

где _i - корни характеристического уравнения, полученного из левой части уравнения (1.6.2) или (1.6.3):

a₀ⁿ+a₁^n-1+...+a_n-1+a_n=0. (1.6.6)

Решение характеристического уравнения зависит от его корней, которые в общем виде могут быть комплексными

_i =  _i  j_i.

Пара мнимых корней (α_i=0 ) характеристического уравнения позволяет получить переходную составляющую в виде автоколебаний с постоянной амплитудой:

Полученные корни характеристического уравнения могут быть представлены в виде точек на комплексной плоскости (рис.4.2.).

(1.6.7)

Рассмотрим лишь две составляющие процесса от пары сопряженных комплексных корней

Y_св(t)=c_ie^{(i+ji)t}+c_i+1e^{(i-ji)t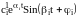}= , (1.6.8)

где c_i, c_i+1, - постоянные коэффициенты;

_i - частота колебаний;

_i - коэффициент затухания;

_i - фаза колебаний.

Анализ (1.6.8) показывает, что это синусоида с амплитудой, изменяющейся по экспоненте . Поэтому, если:

1) _i<0, e^it уменьшается при t, колебание затухает и САУ устойчива (рис.1.6.1,а,б);

2) _i>0, e^it увеличивается при t, колебание увеличивается и САУ неустойчивая (рис.1.6.1,д);

3) _i=0 - незатухающие колебания и САУ на границе устойчивости (рис.1.6.1,а);

4) _i=0 - процесс апериодический (рис.1.6.1,в).

Результаты анализа и виды устойчивости показаны на рис.1.6.1.

Рис.1.6.1. Переходные процессы устойчивых (а,б,в) и неустойчивых (г,д) САУ