
Л16 частотные электрические фильтры
Электрическим фильтром называются четырехполюсники, обычно составленные из катушек индуктивности и конденсаторов, которые пропускают к приемнику из всего спектра источника один или несколько заданных диапазонов частот.
Принцип работы электрофильтров основан на известных положениях: во-первых, что XL прямо пропорционально, а ХС – обратно пропорционально частоте и, во вторых, что в индуктивном сопротивлении I на /2 отстает от U, а в емкостном опережает. Различные комбинации катушек индуктивности и конденсаторов дают фильтры различные по своему действию.
Назовем идеальными фильтры, состоящие из чисто реактивных элементов и будем рассматривать только симметричные фильтры.
Существуют фильтры следующих типов: низкочастотные, высокочастотные, полосные, многополосные и заграждающие. Фильтры обычно собираются из реактивных сопротивлений по симметричной Т или П – схеме.
Приведенная классификация фильтров – не единственная. Фильтры еще различаются на следующие типы: фильтры типа k (у которых произведение продольного сопротивления на поперечное некоторое постоянное число k), типа m (у них это произведение число переменное), мостовые фильтры; фильтры образованные индуктивно связанными цепями, кварцевые фильтры, RС фильтры, активные фильтры и т.д.
Низкочастотные фильтры пропускают токи с частотами от 0 до 0, высокочастотные – токи с частотами от 0 до . Полосные фильтры пропускают токи, частоты которых лежат в пределах от 1 до 2, а многополосные – токи одновременно нескольких диапазонов частот от 1 до 2 от 3 до 4 и т.д.
Заграждающие фильтры пропускают токи с частотами от 0 до 1 и от 2 до .
Поскольку фильтры - частный случай четырехполюсника, то его свойства определяются вторичными параметрами ZС и постоянной передачи g=a+jb, где
а – коэффициент затухания;
b – коэффициент фазы.
Областью пропускания фильтра называют диапазон частот в котором а=0. Областью затухания фильтра называют диапазон частот, в котором а0.
В области пропускания I и U на выходе и входе фильтры д.б. одинаковыми по величине. Это было бы возможно, если бы фильтр был согласован с нагрузкой, т.е. ZH=ZC во всем диапазоне его пропускания, что однако принципиально не возможно.
При согласовании фильтра с нагрузкой токи и напряжения входа I1;U1; и выхода I2;U2 связаны соотношением:
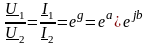 .
.
Тогда при а=0, имеем
U1=U2; I1=I2.
Если же оба условия Z2=ZC и а=0 одновременно выполнимы не будут, то величины токов и напряжений на входе и выходе уже не будут одинаковы.
Таким образом, в области пропускания фильтра (а=0) равенство I и U на входе и выходе получается только для одной или нескольких частот. В области затухания даже для идеальных фильтров а. Для получения резкого увеличения «а» в области затухания пользуются многозвенными фильтрами, состоящими из нескольких включенных в каскад П – или Т – звеньев или фильтров с более сложными схемами ( например типа m).
3.10.1. Низкочастотные фильтры
ФНЧ, собранные по П- или Т- схеме представлены на рис.3.10.
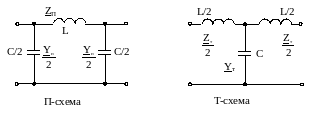
Рис. 3.10. Схемы фильтров низких частот
Из теории четырехполюсников записанных в А- форме записи
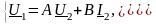 (3.26)
(3.26)
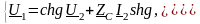 (3.27)
(3.27)
Из сравнения (3.26) и (3.27)
A=chg=ch(a+jb). (3.28)
Для П- и Т- схем:
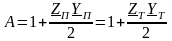 , (3.29)
, (3.29)
где
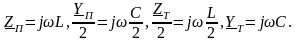
В соответствии с этим для П- и Т- схем:
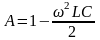 . (3.30)
. (3.30)
Из (3.30) видно, что А – положительное или отрицательное действительное число.
Из (3.28)
A=ch(a+jb)=chacosb+jshasinb. (3.31)
Уравнение (3.31) распадается на два уравнения:
 (3.32)
(3.32)
Определим границы области пропускания. При а=0, cha=1, тогда
+1А=cos b -1, (3.33)
или
 , (3.34)
, (3.34)
следовательно фильтр пропускает без затухания частоты от =0 до граничной частоты
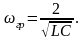 (3.35)
(3.35)
Найдём изменение коэффициентов фазы ”b” в области пропускания фильтра.
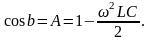
Введём
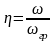 ,
тогда
,
тогда
cos b=1-22. (3.36)
Для области затухания =1
Из (3.32) shasin b=0 – так как в области затухания а0, то
sin b=0; b= (рис.3.11).
Для области затухания из первого равенства (3.32):
cha = -A=22-1. (3.37)
Из (3.37) подставляя от 1 до определяем cha, а затем “a” (рис.3.11).
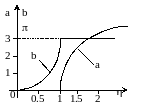
Рис.3.11. График коэффициентов затухания и фазы для ФНЧ
Рассмотрим поведение характеристического сопротивления Zc для ФНЧ, собранных по Т и П - схеме.
Для
симметричного четырёхполюсника
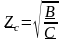 ,
,
для
Т-схемы -
 ,
, ,
,
для
П-схемы -
 ,
,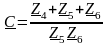 .
.
Подставляя выражения для коэффициентов В и С в уравнение характеристического сопротивления и вводя относительную частоту , получим уравнения характеристического сопротивления для ФНЧ, собранного по П-схеме- Zсп и Т-схеме - Zст.
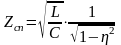 , (3.38)
, (3.38)
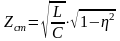 . (3.39)
. (3.39)
В уравнениях (3.38), (3.39) при большой единицей можно пренебречь (область затухания) и тогда
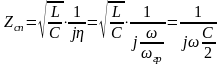 -имеет
емкостной характер (рис.3.12)
-имеет
емкостной характер (рис.3.12)
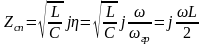 -имеет
индуктивный характер (рис.3.12)
-имеет
индуктивный характер (рис.3.12)
В области пропускания 0 1 поэтому Zст и Zсп носят чисто активный характер (рис.3.12).
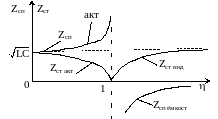
Рис. 3.12. Графики изменения характеристического сопротивления ФНЧ, собранных по Т и П –схеме
Применение той или иной схемы ФНЧ определяется условиями его работы и предъявляемыми к нему требованиями.
