3.4.3. Несимметричный режим трехфазной цепи, соединенной треугольником

Если на выводах трехфазной нагрузки, соединенной треугольником, заданы линейные напряжения U_AB, U_BC, U_CA (рис.3.5), то токи в фазах нагрузки равны:

(3.19)

Токи в линии определяются по уравнениям (3.6).

Если на выводах несимметричной трехфазной нагрузки, соединенной треугольником, заданы фазные напряжения U_А, U_В, U_С источника, соединенного звездой, то линейные напряжения определяются как разности фазных напряжений. Токи в фазах нагрузки и в линии определяются по уравнениям (3.19) и (3.6).

3.4.4. Мощность несимметричной трехфазной цепи

Комплексная мощность четырехпроводной несимметричной трехфазной цепи

, (3.20)

где активная мощность P=U_AI_Acos_A+U_BI_Bcos_B+U_CI_Ccos_C. Для измерения трех слагаемых активной мощности необходимы три ваттметра, включенные по схеме на рис. 3.11.

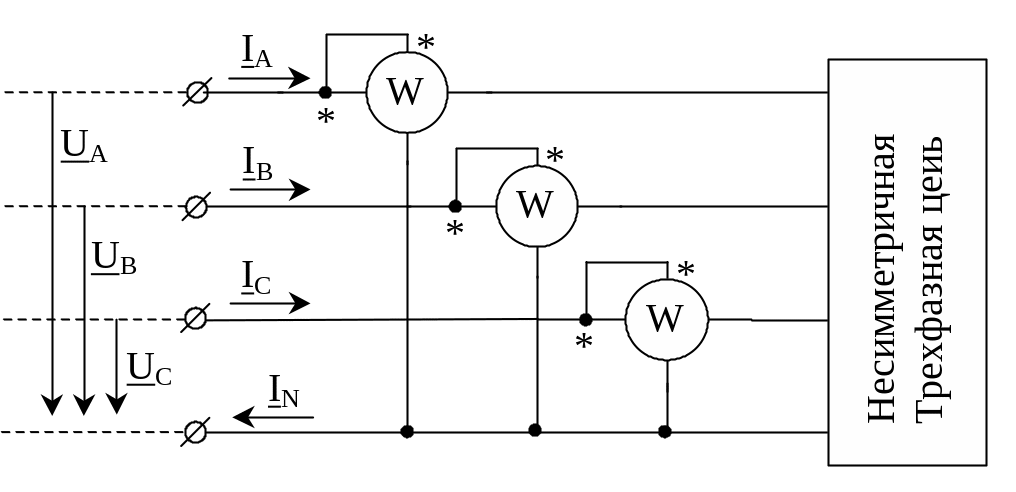
Рис.3.11. Измерение мощности в трехфазной цепи с нулевым проводом

В уравнении (3.20) исключим ток в фазе С.

.

.

Тогда активная мощность

. (3.21)

Для измерения двух слагаемых в уравнении (3.21) необходимы два ваттметра, включенные по схеме на рис.3.12.

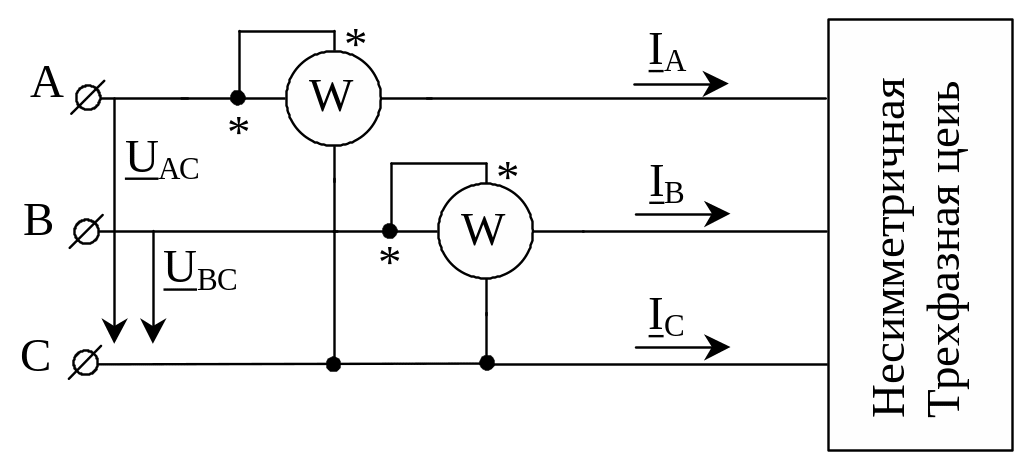
Рис.3.12. Измерение мощности в трехфазной цепи без нулевого провода

3.5. Вращающееся магнитное поле

Возможность создания вращающегося магнитного поля является важным свойством трехфазной цепи. На рис. 3.13. показана катушка, по которой проходит синусоидальный ток. Буква Н означает начало, а К - конец катушки.

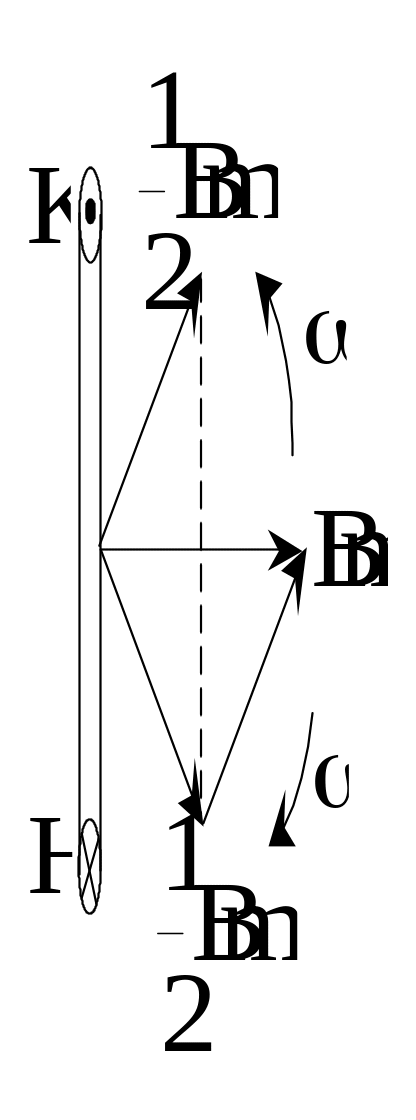
Рис.3.13. Разложение пульсирующего магнитного поля на две составляющие

Направление вектора магнитной индукции определяется направлением намотки катушки и направлением тока в ней в данный момент времени. Вектор магнитной индукции направлен так, как показано на рис. 3.13. В следующий полупериод, когда ток отрицателен, вектор направлен в противоположную сторону. Таким образом геометрическим местом конца вектора является ось катушки. Пульсирующую магнитную индукцию можно рассматривать как результат совместного действия двух составляющих, вращающихся в противоположных направлениях с половинной амплитудой и одинаковой угловой скоростью .

.

Магнитную индукцию, вращающуюся со скоростью , можно получить, если с помощью второй катушки с гармоническим током, сдвинутой относительно первой в пространстве, компенсировать составляющую обратного вращения первой катушки.

Большое удобство, с точки зрения возможности получения кругового вращающегося поля, представляет трехфазный ток.

Расположим три одинаковые катушки так, чтобы их оси были сдвинуты относительно друг друга на 120° и подключим их к трехфазной цепи (рис. 3.14.).

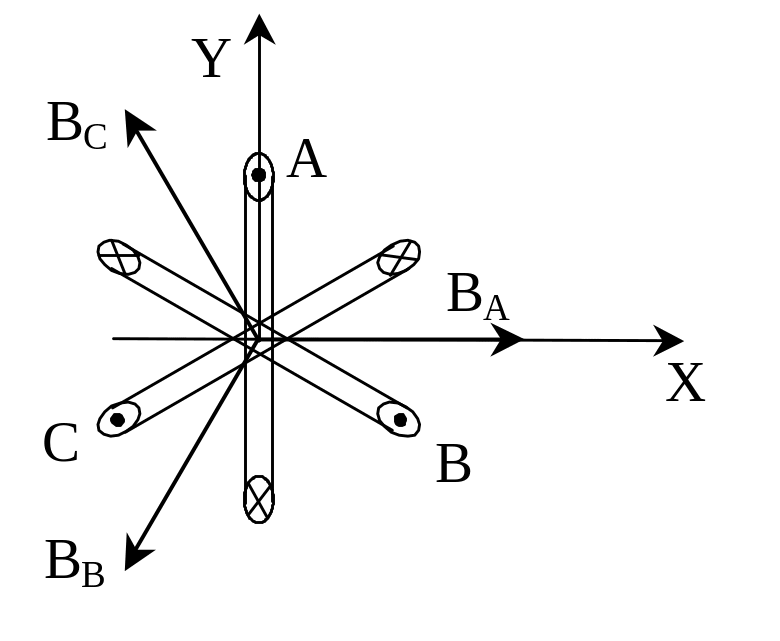
Рис.3.14. Получение вращающегося магнитного поля

Направление потоков по отношению к выбранному направлению токов определяем по правилу правоходового винта.

Мгновенное значение индукции в фазах:

B_A(t)=B_msint,

B_B(t)=B_msin(t-120⁰), (3.22)

B_C(t)=B_msin(t+120⁰).

Для образования общего магнитного поля эти индукции складываются. Проведем оси Х и У (рис. 3.14.). Определим составляющую результирующего магнитного поля на ось Х в момент времени t=0.

.

Подставим выражение индукции как синусоидальных величин:

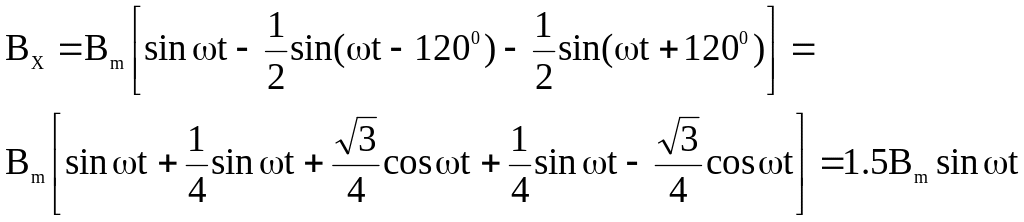
Составляющая результирующего поля по оси У при t =0:

.

Подставим значение индукции как синусоидальных величин:

.

Результирующая магнитная индукция:

. (3.23)

Угол  = t, образуемый им с осью У, равен:

. (3.24)

Полученные выражения показывают, что результирующий вектор магнитного поля имеет постоянный модуль 1,5 В_m (3.23) и равномерно вращается с угловой скоростью  (3.24).

Ось результирующего магнитного поля совпадает с осью той катушки, в которой ток имеет наибольшее значение. Направление вращения поля соответствует чередованию максимальных значений тока в катушках А, В, С, т.е. совпадает с порядком чередования фаз в питающей сети, поэтому, если поменять местами концы двух любых питающих проводов, то направление вращения поля изменится на противоположное.

При несимметрии токов в катушках вместо кругового вращающегося поля получается эллиптическое.

Принцип действия асинхронных машин основан на явлениях, связанных с вращающимся магнитным полем.