3.4. Несимметричный режим трехфазной цепи

Несимметрия в трехфазной цепи может быть вызвана различными причинами: несимметричной нагрузкой, коротким замыканием или размыканием фазы, неравенством Э.Д.С. и т.д.

3.4.1. Несимметричный режим трехфазной цепи, соединенной звездой с нейтральным проводом

Пусть заданы несимметричные фазные напряжения U_A, U_B, U_C на зажимах несимметричного приемника (рис. 3.8.). Заданные напряжения можно приписать источникам Э.Д.С.: E_A=U_A, E_B=U_B, E_C=U_C.

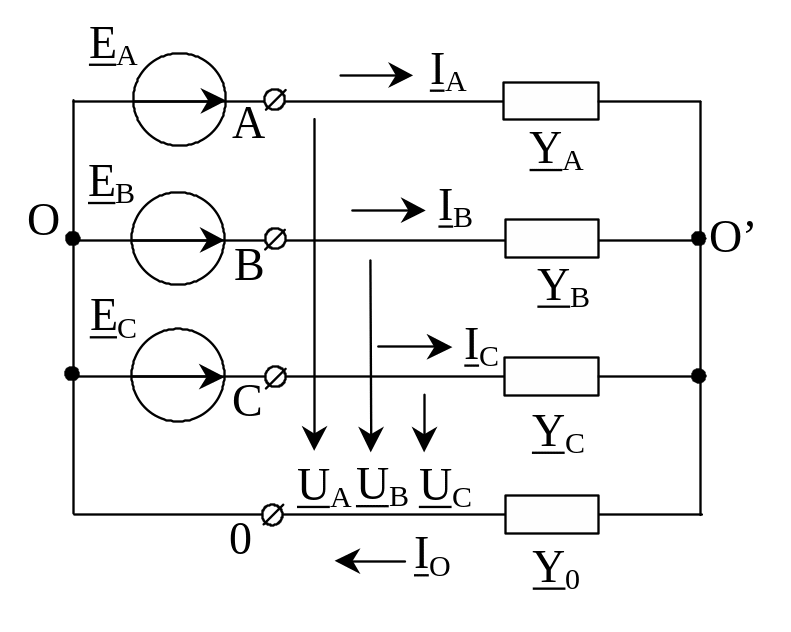
Рис.3.8. Схема несимметричной нагрузки, соединенной по схеме звезды с нулевым проводом

Обозначая напряжение между нулевыми точками U_O’O, по методу двух узлов запишем

, (3.10)

где -проводимости ветвей нагрузки, -проводимость нулевого провода.

Токи в ветвях и нулевом проводе:

, ,

, .

При симметричной системе токов Y_A=Y_B=Y_C=Y нулевой провод можно удалить Y₀=0, и это не повлияет на фазные напряжения нагрузки. В этих условиях напряжение смещения нейтрали:

.

3.4.2. Несимметричный режим трехфазной цепи, соединенной звездой при отсутствии нейтрального провода

При отсутствии нейтрального провода обычно бывают заданы не фазные, а линейные напряжения на зажимах цепи U_AB, U_BC, U_CA. Обозначим фазные напряжения на выходах нагрузки через U_AH, U_ВН, U_CH и определим токи в фазах I_A=Y_AU_AH, I_В=Y_BU_BH, I_C= Y_CU_CH, где Y_A, Y_B, Y_C -проводимости фаз нагрузки .

По первому закону Кирхгофа:

I_A+ I_B+ I_C=0,

или

Y_AU_AH+ Y_BU_BH+ Y_CU_CH=0. (3.11)

Выразим фазные напряжения U_BH, U_СH через U_AH и заданные линейные напряжения:

U_BH= U_AH - U_AB, U_СH= U_AH+ U_СA. (3.12)

Подставим (4.12) в (4.11) и определим

. (3.13)

Определим U_AH, U_BH через U_CH и линейные напряжения, и U_СH, U_АH через U_ВH и линейные напряжения:

(3.14)

(3.15)

Подставляя поочередно (3.14) и (3.15) в уравнение (3.11) и определим фазные напряжения:

(3.16)

По найденным фазным напряжениям нагрузки (3.13, 3.16) находят фазные токи. Распределение напряжения между сопротивлениями несимметричной звезды иллюстрирует векторная диаграмма цепи (рис. 3.9).

Рис.3.19. Векторная диаграмма, иллюстрирующая смещение нейтрали при изменении нагрузки в фазе А

Начальной точкой диаграммы служит нулевая точка (0) - нейтраль генератора, из которой строятся три вектора фазных напряжений генератора U_A, U_B, U_C. Линейные напряжения генератора соединяют концы фазных. Нейтраль 0 находится в центре треугольника линейных напряжений. Пока сопротивления нагрузки в фазах одинаковы Y_A=Y_B=Y_C=Y нулевая точка генератора (0) и приемника (О^’) совпадают. Несимметрия нагрузки вызывает несимметрию ее фазных напряжений и смещение ее нулевой точки О^’ из центра треугольника.

Рассмотрим случай, когда нагрузка состоит из активных проводимостей и две из них одинаковы q_B=q_C=q , а активная проводимость q_A изменяется от 0 до . Обозначим отношение и выразим напряжение смещения нейтрали следующим образом:

Из основного свойства фазового оператора (4.3)

а²+а=-1.

Тогда

(3.17)

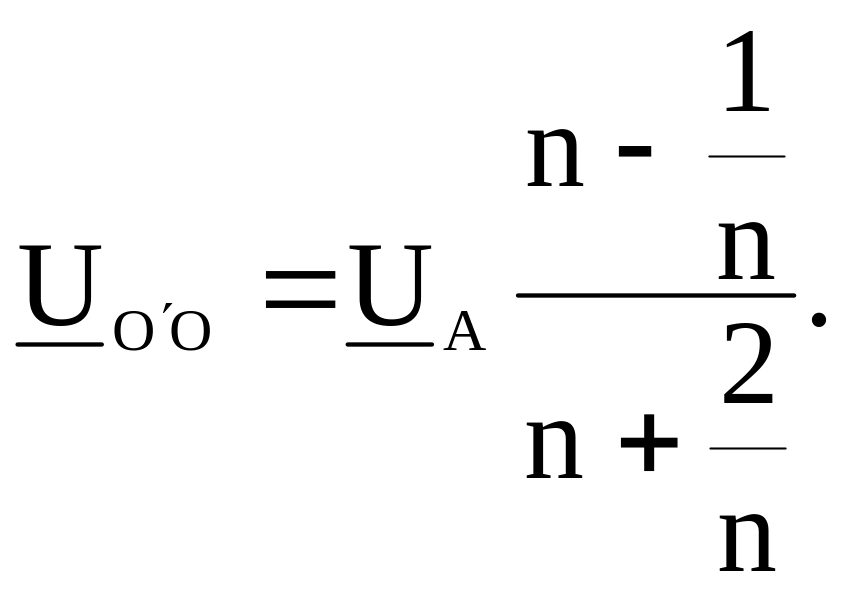(3.18)

При изменении q_А от 0 до  множитель при U_A остается действительным числом, следовательно напряжение смещения нейтрали U_O’O совпадает по фазе с U_A. При n>1 вектор U_O’O совпадает по направлению с U_A, а при n<1 -противоположен ему. Геометрическое место точки 0 - перпендикуляр, опущенный из точки А на противоположную сторону. При холостом ходе q_A=0 и n=0, тогда из уравнения (3.17) .

В этом случае фазные напряжения нагрузки

,

,

.

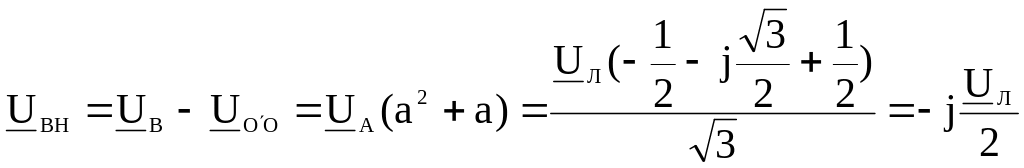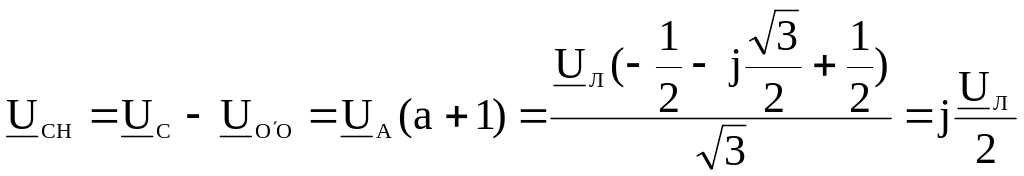При коротком замыкании q_A= и n=0, тогда из уравнения (3.18) U_O’O=U_A.

Фазные напряжения нагрузки:

U_AH=U_A-U_O’O=0,

U_BH=U_B-U_O’O=U_B-U_A=U_BA=-U_AB,

U_C=U_C-U_O’O=U_C-U_A=U_CA.

Из уравнений следует, что при к. з. фазное напряжение на нагрузке U_BH равно линейному U_AB и противоположно ему по направлению, напряжение U_BH равно линейному U_CA.

Если сопротивления фаз различны по характеру, то направление смещения нейтрали зависит от последовательности чередования фаз и это имеет большое практическое значение, в качестве примера рассмотрим схему фазоуказателя, которую используют для определения чередования фаз, состоящую из конденсатора и двух одинаковых электрических ламп, соединенных звездой (рис. 3.10).

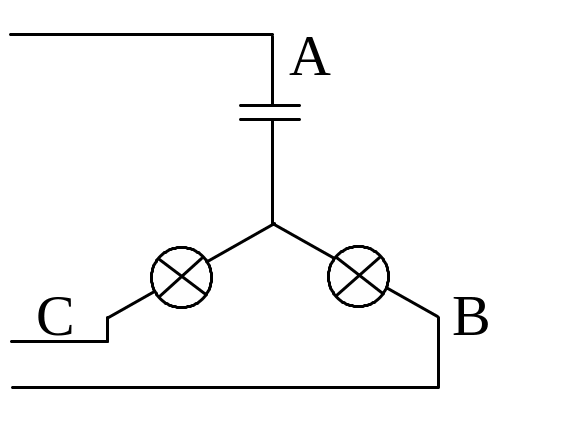
Рис.3.10. схема фазоуказателя

Конденсатор присоединен к фазе А, лампы - к фазам В и С. Емкостное сопротивление конденсатора берется равным по модулю сопротивлению ламп, т.е. Z_А=-jX_C, Z_B=Z_С=R, X_C=R. Неравенство напряжений на лампах проявится в том, что накал ламп будет разным. Покажем это, определив отношение напряжения в фазе В к напряжению в фазе С, используя систему уравнений (3.16).

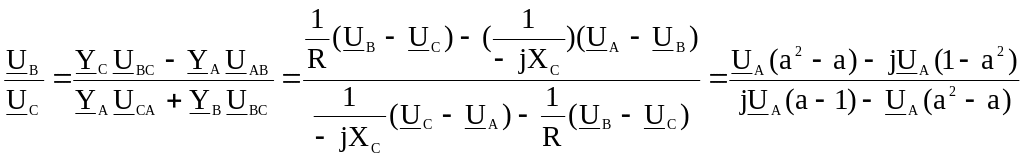
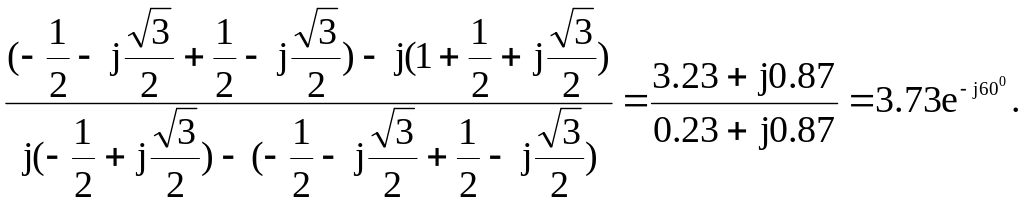
Следовательно, лампа, присоединенная к фазе В, будет светится ярче лампы, присоединенной к фазе С. Вместо конденсатора можно применить индуктивность. Тогда лампа, включенная в фазу С, будет гореть ярче лампы в фазе В.