3.3.1. Симметричный режим работы трехфазной цепи, при соединении генератора и нагрузки звездой (рис. 3.4.)

Токи в фазах

Ток в нейтральном проводе отсутствует.

.

Поэтому при симметричном приемнике нейтральный провод не применяют. Линейные напряжения определяются как разности фазных напряжений:

U_AB=U_A-U_B, U_BC=U_B-U_C, U_CA=U_C-U_A.

Векторная диаграмма токов и напряжений при симметричном режиме для схемы (рис.3.4.) и индуктивном характере нагрузки (0) показана на рис.3.6.

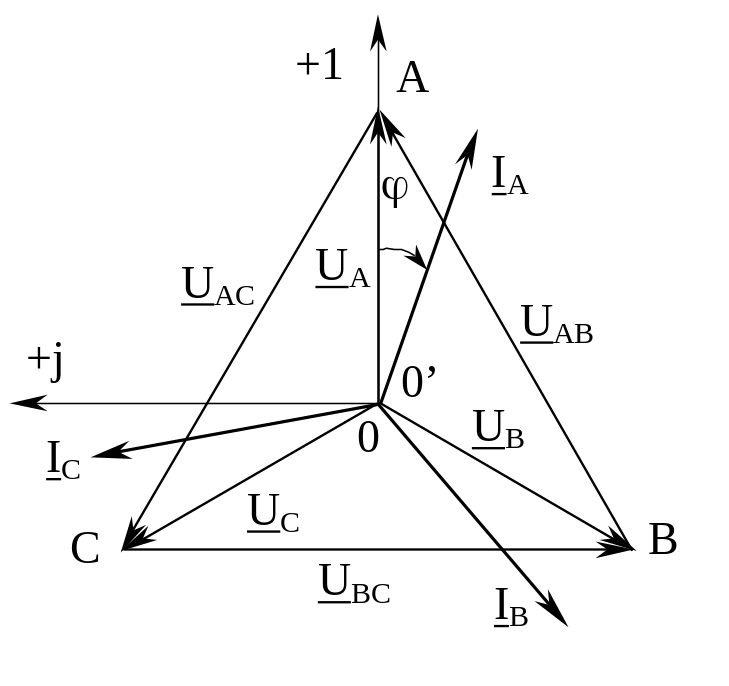
Рис.3.6. Векторная диаграмма симметричного режима при соединении индуктивной нагрузки и генератора звездой

В любом месте трехфазной линии при симметричном режиме модуль

. (3.5)

Действительно .

3.3.2. Симметричный режим работы трехфазной цепи, при соединении генератора и нагрузки треугольником (рис. 3.5.)

При соединении треугольником линейные токи определяются как разности фазных токов:

I_A=I_AB-I_CA, I_B=I_BC-I_AB, I_C=I_CA-I_BC. (3.6)

Для построения векторной диаграммы возьмем три вектора линейных напряжений (рис. 3.7.).

Рис.3.7. Векторная диаграмма симметричного режима при соединении индуктивной нагрузки Z и генератора треугольником

Углы между линейными напряжениями (они являются вместе с тем фазными) равны 120°. По отношению к этим напряжениям соответствующие векторы фазных токов I_AB, I_BC, I_CA сдвинуты по фазе на углы , величина которых зависит от характера фазной нагрузки. Чтобы построить вектор линейного тока, например, I_A на основании соотношений (4.6), нужно к вектору фазного I_AB прибавить вектор (-I_CA), т.е. вектор, равный по длине I_CA , но противоположный по направлению. Так же строятся и остальные векторы линейных токов.

При симметричном режиме векторы фазных и линейных токов образуют три равнобедренных треугольника с острыми углами 30°. В одном из этих треугольников опустим перпендикуляр из вершины тупого угла на противоположную сторону (рис. 3.7.), найдем, что .

Следовательно, при соединении треугольником:

. (3.7)

При расчете токов трехфазной цепи в данном случае, сначала определяют фазные токи:

.

Затем по уравнению (3.7) определяют линейные токи:

.

Рассматривая способы соединения звездой и треугольником следует иметь в виду, что приемники могут включаться звездой или треугольником независимо от соединения обмоток генератора.

Проанализируем как изменяются токи симметричной нагрузки, имеющей постоянное фазное сопротивление Z при переключении со звезды на треугольник. Такое переключение осуществляется посредством трехполюсного переключателя. При соединении звездой фазный ток I_Фз, равен линейному

.

Так как соединение звездой , то линейный ток при этом соединении

. (3.8)

При соединении треугольником , но линейный ток треугольника , следовательно:

. (3.9)

Сопоставим уравнения (4.8) и (4.9), получим, что при одном и том же U_Л и одинаковом Z

.

Для фазных токов:

.

3.3.3. Активная, реактивная и полная мощности трехфазной симметричной системы

Активной мощностью трехфазной системы называется сумма активных мощностей ее отдельных фаз Р=Р_A+Р_В+Р_С. В симметричной системе фазные мощности равны между собой, поэтому Р=3Р_Ф. Для каждой фазы Р_Ф=U_ФI_Фcos, где  - угол сдвига фаз между фазными напряжением и током.

При соединении звездой I_Л = I_Ф, .

При соединении треугольником , U_Л=U_Ф.

В обоих случаях, заменяя в выражении для активной мощности фазные величины на линейные, получим для мощности одно и тоже выражение:

.

Аналогично для реактивной мощности

,

для полной мощности